Tag Archives: Davide Leonessi

Infinite Hex is a draw

Posted on by
Reply

[bibtex key=”HamkinsLeonessi:Infinite-Hex-is-a-draw”]

Download the article at https://arxiv.org/abs/2201.06475.

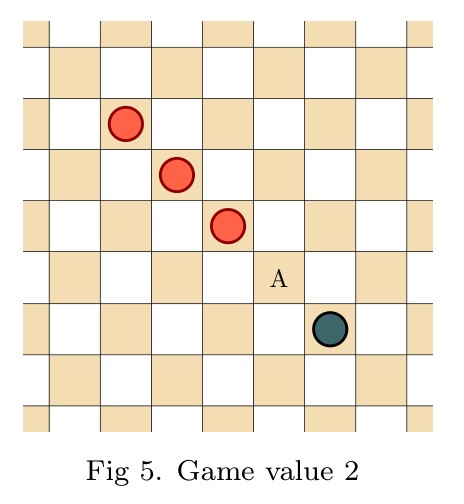
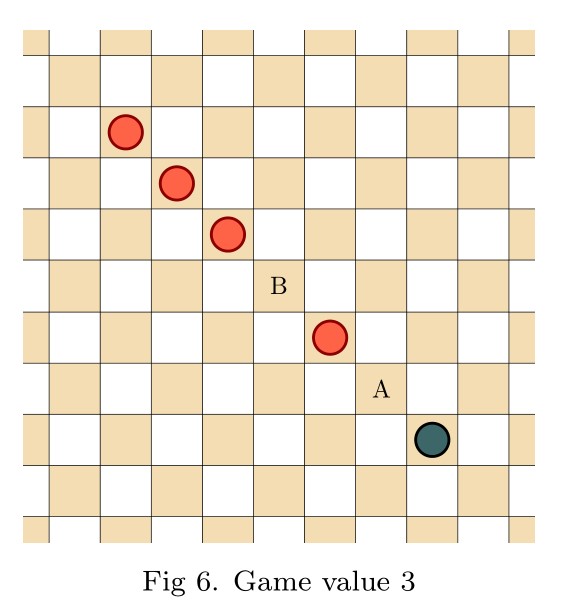
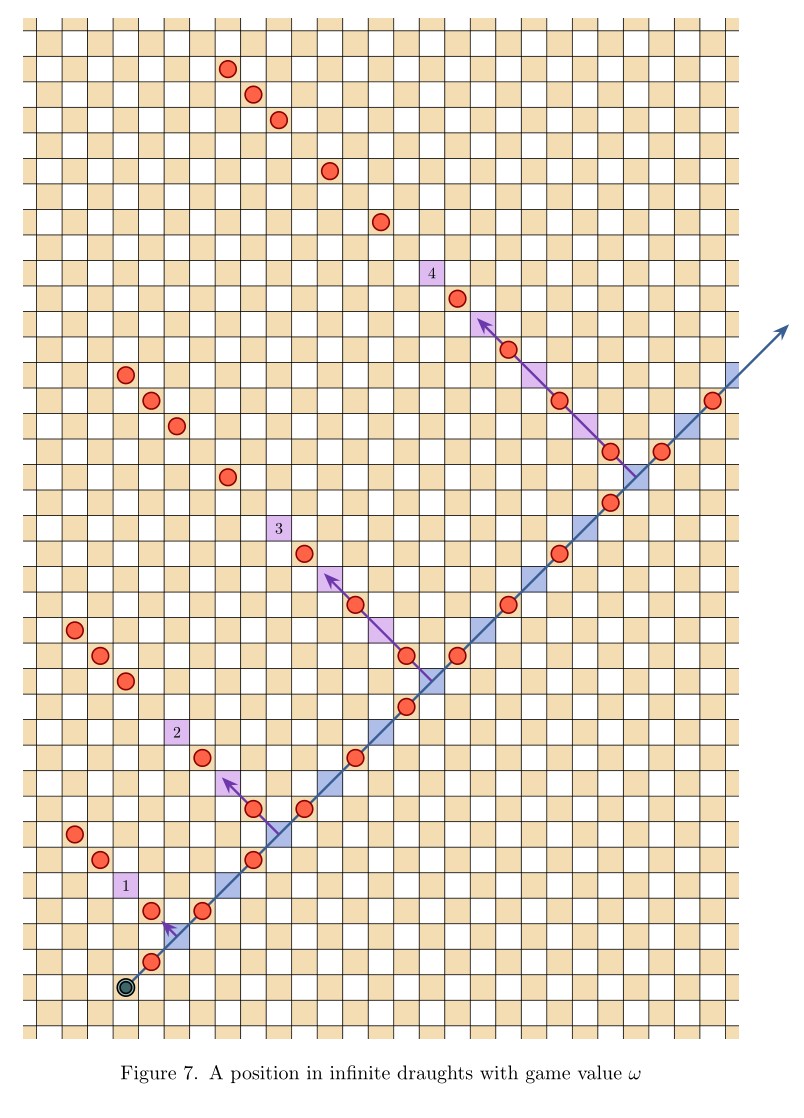
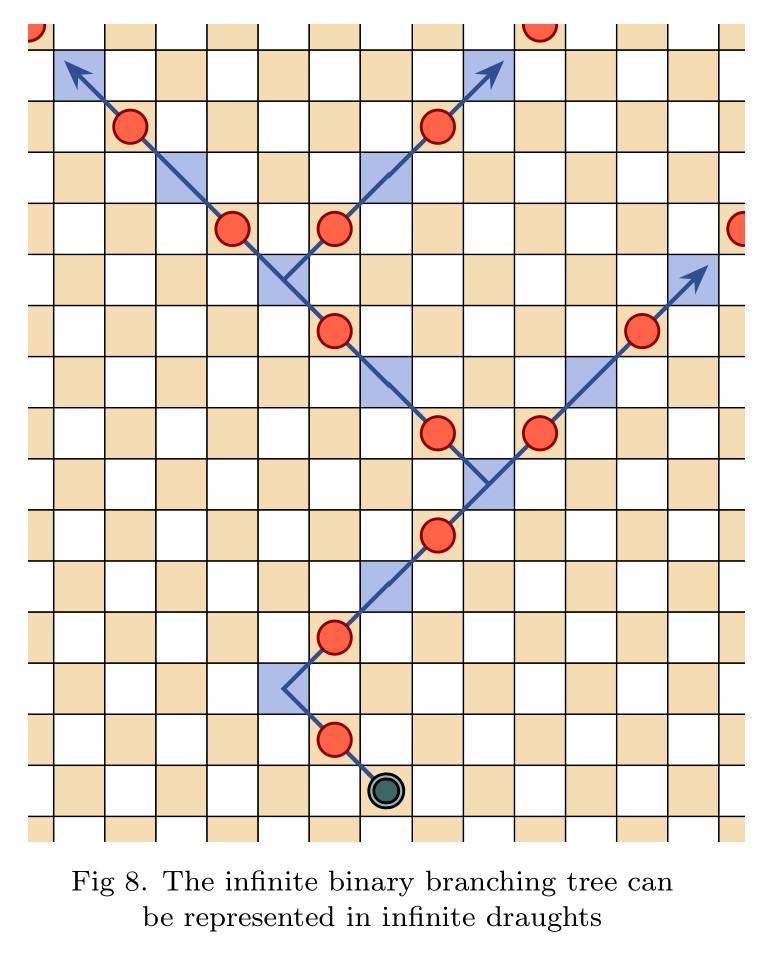
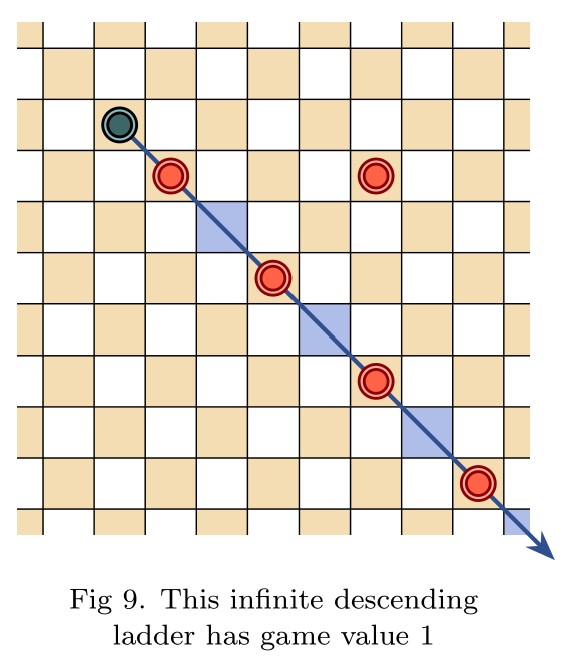
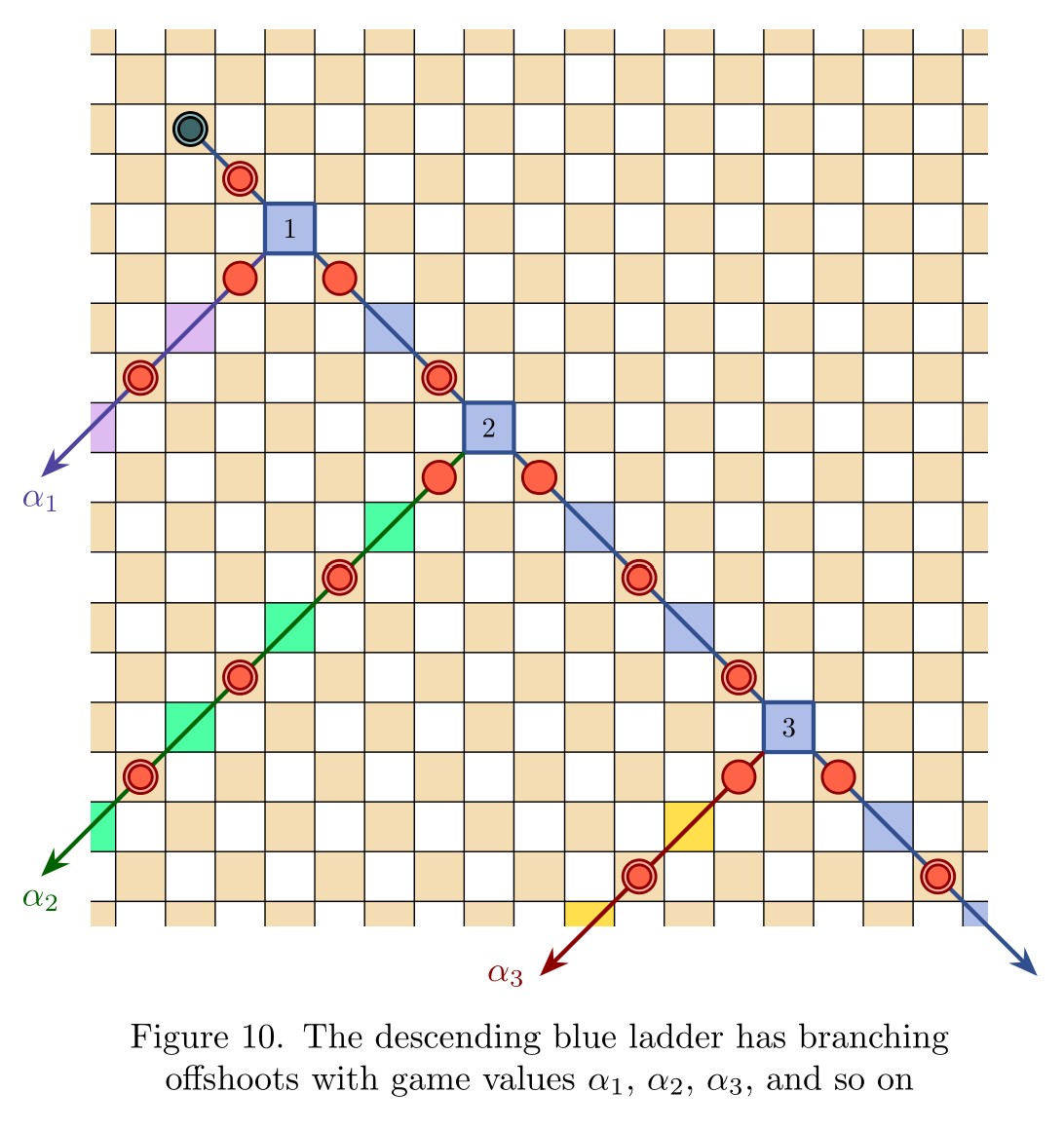
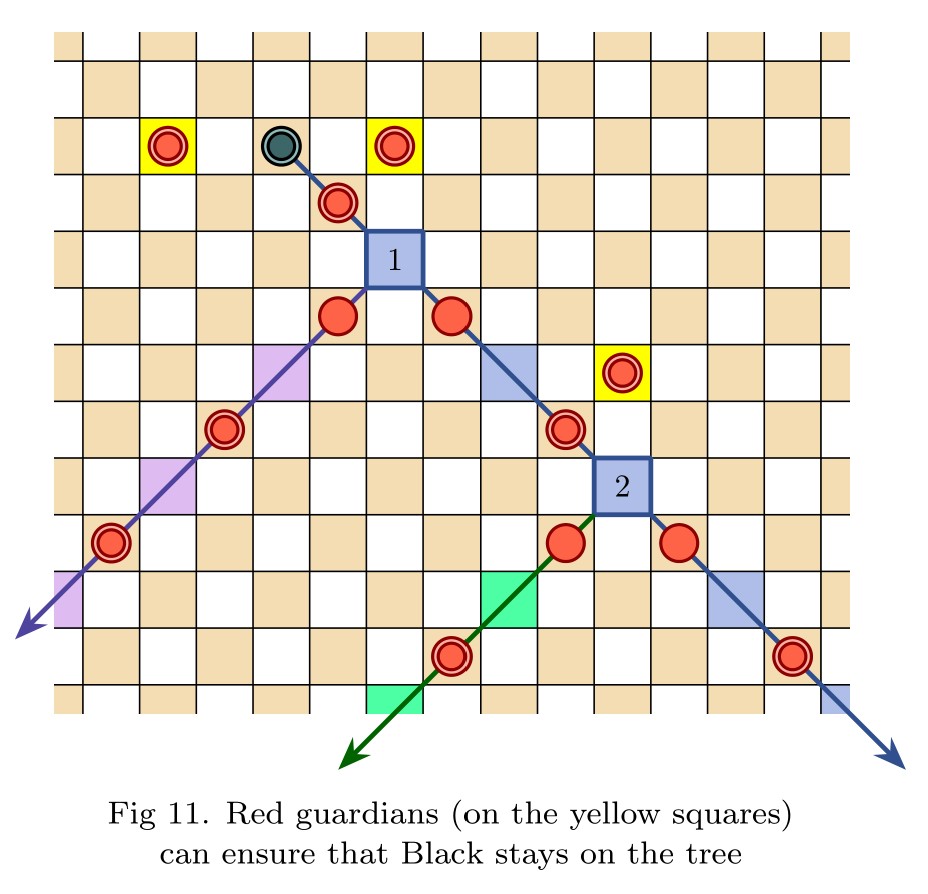
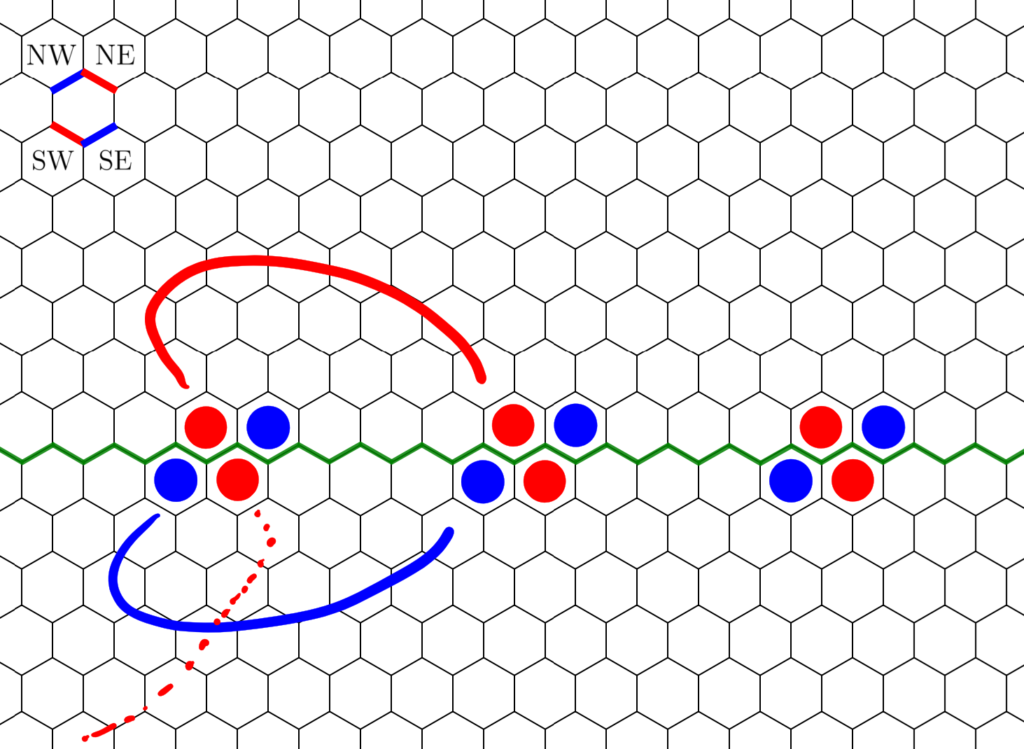
Abstract. We introduce the game of infinite Hex, extending the familiar finite game to natural play on the infinite hexagonal lattice. Whereas the finite game is a win for the first player, we prove in contrast that infinite Hex is a draw—both players have drawing strategies. Meanwhile, the transfinite game-value phenomenon, now abundantly exhibited in infinite chess and infinite draughts, regrettably does not arise in infinite Hex; only finite game values occur. Indeed, every game-valued position in infinite Hex is intrinsically local, meaning that winning play depends only on a fixed finite region of the board. This latter fact is proved under very general hypotheses, establishing the conclusion for all simple stone-placing games.

This is my second joint project with Davide Leonessi, the first being our work on Transfinite games values in infinite draughts, both projects growing out of his work on his MSc in MFoCS at Oxford, for which he earned a distinction in September 2021.

Here is a convenient online Hex player, for those who want to improve their game: http://www.lutanho.net/play/hex.html.

Infinite draughts and the logic of infinitary games, Oslo, November 2021

Posted on by
Reply

This will be a talk 11 November 2021 for the Oslo Seminar in Mathematical Logic, meeting online via Zoom at 10:15am CET (9:15am GMT) at Zoom: 671 7500 0197

Abstract. I shall give an introduction to the logic of infinite games, including the theory of transfinite game values, using the case of infinite draughts as a principal illustrative instance. Infinite draughts, also known as infinite checkers, is played like the finite game, but on an infinite checkerboard stretching without end in all four directions. In recent joint work with Davide Leonessi, we proved that every countable ordinal arises as the game value of a position in infinite draughts. Thus, there are positions from which Red has a winning strategy enabling her to win always in finitely many moves, but the length of play can be completely controlled by Black in a manner as though counting down from a given countable ordinal. This result is optimal for games having countably many options at each move—in short, the omega one of infinite draughts is true omega one.

Infinite-draughts-Oslo-2021Download

Transfinite game values in infinite draughts

Posted on by
3

A joint paper with Davide Leonessi, in which we prove that every countable ordinal arises as the game value of a position in infinite draughts, and this result is optimal for games having countably many options at each move. In short, the omega one of infinite draughts is true omega one.

[bibtex key=”HamkinsLeonessi:Transfinite-game-values-in-infinite-draughts”]

Download the paper at arXiv:2111.02053

Abstract. Infinite draughts, or checkers, is played just like the finite game, but on an infinite checkerboard extending without bound in all four directions. We prove that every countable ordinal arises as the game value of a position in infinite draughts. Thus, there are positions from which Red has a winning strategy enabling her to win always in finitely many moves, but the length of play can be completely controlled by Black in a manner as though counting down from a given countable ordinal.

Davide Leonessi, MSc MFoCS, Oxford, September 2021

Posted on by
1

Mr. Davide Leonessi successfully defended his dissertation for the Masters of Science degree in Mathematics and Foundations of Computer Science, entitled “Transfinite game values in infinite games,” on 15 September 2021. Davide earned a distinction for his thesis, an outstanding result.

Davide Leonessi | Google scholar | Dissertation | arXiv

Abstract. The object of this study are countably infinite games with perfect information that allow players to choose among arbitrarily many moves in a turn; in particular, we focus on the generalisations of the finite board games of Hex and Draughts.

In Chapter 1 we develop the theory of transfinite ordinal game values for open infinite games following [Evans-Hamkins 2014], and we focus on the properties of the omega one, that is the supremum of the possible game values, of classes of open games; we moreover design the class of climbing-through-$T$ games as a tool to study the omega one of given game classes.

The original contributions of this research are presented in the following two chapters.

In Chapter 2 we prove classical results about finite Hex and present Infinite Hex, a well-defined infinite generalisation of Hex.

We then introduce the class of stone-placing games, which captures the key features of Infinite Hex and further generalises the class of positional games already studied in the literature within the finite setting of Combinatorial Game Theory.

The main result of this research is the characterization of open stone-placing games in terms of the property of essential locality, which leads to the conclusion that the omega one of any class of open stone-placing games is at most $\omega$. In particular, we obtain that the class of open games of Infinite Hex has the smallest infinite omega one, that is $\omega_1^{\rm Hex}=\omega$.

In Chapter 3 we show a dual result; we define the class of games of Infinite Draughts and explicitly construct open games of arbitrarily high game value with the tools of Chapter 1, concluding that the omega one of the class of open games of Infinite Draughts is as high as possible, that is $\omega_1^{\rm Draughts}=\omega_1$.

The full dissertation is available:

Transfinite-game-values-in-infinite-gamesDownload