In this post I’d like to explain a certain aspect of my on-going project with Makoto Kikuchi on set-theoretic mereology, which is set theory, undertaken in the full set-theoretic universe 𝑉, but using only the inclusion (subset) relation ⊆, rather than the element-of relation ∈.  (See my earlier post, Different models of set theory with the same subset relation) The subset relation is of course a partial order and indeed a lattice order, since any two sets 𝑎 and 𝑏 have a least upper bound, the union 𝑎 ∪𝑏, and a greatest lower bound, the intersection 𝑎 ∩𝑏. Furthermore, the lattice has a least element ∅, but no greatest element, and for any set 𝑎, the collection of sets with ∅ ⊆𝑏 ⊆𝑎 forms an atomic Boolean algebra.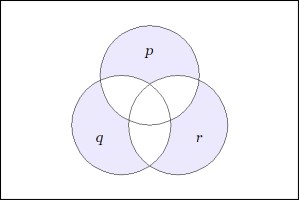To assist with the analysis, let’s work a bit more generally. Recall that a partial order is a lattice order, if any two elements have a least upper bound (join) and greatest lower bound (meet), which I shall denote by 𝑎 ∪𝑏 and 𝑎 ∩𝑏, respectively, since I am interested in the set-theoretic cases; similarly, I’ll denote the order by 𝑎 ⊆𝑏. Let me define that a lattice is locally Boolean, if there is a least element 0, and for every 𝑎, the interval [0,𝑎] is a Boolean algebra. Such a lattice is unbounded, if there is no maximal element. In such a lattice, an atom is a non-zero element that is minimal above 0, and the lattice is atomic, if every element is the least upper bound of the atoms below it. For each natural number 𝑛, let us introduce the unary predicate denoted |𝑥| ≥𝑛, which expresses that 𝑥 admits a decomposition as the join of 𝑛 distinct nonzero incompatible elements: 𝑥 =𝑦1 ∪⋯ ∪𝑦𝑛, where 𝑦𝑖 ≠0 and 𝑦𝑖 ∩𝑦𝑗 =0 for 𝑖 ≠𝑗. In an atomic locally Boolean lattice, the relation |𝑥| ≥𝑛 holds just in case there are at least 𝑛 atoms 𝑎 ≤𝑥.

To give a few examples, if HF is the set of hereditarily finite sets, then ⟨HF, ⊆⟩, using the usual subset relation, is an unbounded atomic locally Boolean lattice. More generally, if 𝑉 is any model of set theory (even a very weak theory is sufficient), then ⟨𝑉, ⊆⟩ is an unbounded atomic locally Boolean lattice.

I should like to prove here that the theory of unbounded atomic locally Boolean lattice orders is decidable, and furthermore admits elimination of quantifiers down to the language including the Boolean operations and the relations expressing the height or size of an object, |𝑥| ≥𝑛 and |𝑥| =𝑛.

Theorem. Every formula in the language of lattices is equivalent, over the theory of unbounded atomic locally Boolean lattices, to a quantifier-free formula in the language of the order 𝑎 ⊆𝑏, equality 𝑎 =𝑏, meet 𝑎 ∩𝑏, join 𝑎 ∪𝑏, relative complement 𝑎 −𝑏, constant 0, the unary relation |𝑥| ≥𝑛, and the unary relation |𝑥| =𝑛, where 𝑛 is respectively any natural number.

Proof. We prove the result by induction on formulas. The collection of formulas equivalent to a quantifier-free formula in that language clearly includes all atomic formulas and is closed under Boolean combinations. So it suffices to eliminate the quantifier in a formula of the form ∃𝑥 ⁢𝜑⁡(𝑥,…), where 𝜑⁡(𝑥,…) is quantifier-free in that language. Let us make a number of observations that will enable various simplifying assumptions about the form of 𝜑.

Because equality of terms is expressible by the identity 𝑎 =𝑏 ⟺ 𝑎 ⊆𝑏 ⊆𝑎, we do not actually need = in the language (and here I refer to the use of equality in atomic formulas of the form 𝑠 =𝑡 where 𝑠 and 𝑡 are terms, and not to the incidental appearance of the symbol = in the unary predicate |𝑥| =𝑛, which is an unrelated use of this symbol, a mere stylistic flourish). Similarly, in light of the equivalence 𝑎 ⊆𝑏 ⟺ |𝑎 −𝑏| =0, we do not need to make explicit reference to the order 𝑎 ⊆𝑏. So we may assume that all atomic assertions in 𝜑 have the form |𝑡| ≥𝑛 or |𝑡| =𝑛 for some term 𝑡 in the language of meet, join, relative complement and 0. We may omit the need for explicit negation in the formula by systematically applying the equivalences:
¬(|𝑡|≥𝑛)⟺⋁𝑘<𝑛|𝑡|=𝑘 and
¬(|𝑡|=𝑛)⟺(|𝑡|≥𝑛+1)∨⋁𝑘<𝑛|𝑡|=𝑘.
So we have reduced to the case where 𝜑 is a positive Boolean combination of expressions of the form |𝑡| ≥𝑛 and |𝑡| =𝑛.

Let us consider the form of the terms 𝑡 that may arise in the formula. List all the variables 𝑥 =𝑥0,𝑥1,…,𝑥𝑁 that arise in any of the terms appearing in 𝜑, and consider the Venn diagram corresponding to these variables. The cells of this Venn diagram can each be described by a term of the form ⋀𝑖≤𝑁 ±𝑥𝑖, which I shall refer to as a cell term, where ±𝑥𝑖 means that either 𝑥𝑖 appears or else we have subtracted 𝑥𝑖 from the other variables. Since we have only relative complements in a locally Boolean lattice, however, and not absolute complements, we need only consider the cells where at least one variable appears positively, since the exterior region in the Venn diagram is not actually represented by any term. In this way, every term in the language of locally Boolean lattices is a finite union of such cell terms, plus ∅ (which I suppose can be viewed as an empty union). Note that distinct cell terms are definitely representing disjoint objects in the lattice.

Next, by considering the possible sizes of 𝑠 −𝑡, 𝑠 ∩𝑡 and 𝑡 −𝑠, observe that
|𝑠∪𝑡|≥𝑛⟺⋁𝑖+𝑗+𝑘=𝑛(|𝑠|≥𝑖+𝑗)∧(|𝑠∩𝑡|≥𝑗)∧(|𝑡|≥𝑗+𝑘).
Through repeated application of this, we may reduce any assertion about |𝑡| for a term to a Boolean combination of assertions about cell terms. (Note that size assertions about ∅ are trivially settled by the theory and can be eliminated.)

Let us now focus on the quantified variable 𝑥 separately from the other variables, for it may appear either positively or negatively in such a cell term. More precisely, each cell term in the variables 𝑥 =𝑥0,𝑥1,…,𝑥𝑁 is equivalent to 𝑥 ∩𝑐 or 𝑐 −𝑥, for some cell term 𝑐 in the variables 𝑥1,…,𝑥𝑁, that is, not including 𝑥, or to the term 𝑥 −(𝑥1 ∪⋯ ∪𝑥𝑁), which is the cell term for which 𝑥 is the only positive variable.

We have reduced the problem to the case where we want to eliminate the quantifier from ∃𝑥 𝜑, where 𝜑 is a positive Boolean combination of size assertions about cell terms. We may express 𝜑 in disjunctive normal form and then distribute the quantifier over the disjunct to reduce to the case where 𝜑 is a conjunction of size assertions about cell terms. Each cell term has the form 𝑥 ∩𝑐 or 𝑐 −𝑥 or 𝑥 −(𝑥1 ∪⋯𝑥𝑁), where 𝑐 is a cell term in the list of variables without 𝑥. Group the conjuncts of 𝜑 that use the same cell term 𝑐 in this way together. The point now is that assertions about whether there is an object 𝑥 in the lattice such that certain cell terms obey various size requirements amount to the conjunction of various size requirements about cells in the variables not including 𝑥. For example, the assertion ∃𝑥⁡(|𝑥∩𝑐|≥3)∧(|𝑥∩𝑐|≥7)∧(|𝑐−𝑥|=2) is equivalent (over the theory of unbounded atomic locally Boolean lattices) to the assertion |𝑐| ≥9, since we may simply let 𝑥 be all but 2 atoms of 𝑐, and this will have size at least 7, which is also at least 3. If contradictory assertions are made, such as ∃𝑥 ⁡(|𝑥 ∩𝑐| ≥5 ∧|𝑥 ∩𝑐| =3), then the whole formula is equivalent to ⟂, which can be expressed without quantifiers as 0 ≠0.

Next, the key observation of the proof is that assertions about the existence of such 𝑥 for different cell terms in the variables not including 𝑥 will succeed or fail independently, since those cell terms are representing disjoint elements of the lattice, and so one may take the final witnessing 𝑥 to be the union of the witnesses for each piece. So to eliminate the quantifier, we simply group together the atomic assertions being made about the cell terms in the variables without 𝑥, and then express the existence assertion as a size requirement on those cell terms. For example, the assertion ∃𝑥⁡(|𝑐∩𝑥|≥5)∧(|𝑐−𝑥|=6)∧(|𝑑∩𝑥|≥7), where 𝑐 and 𝑑 are distinct cell terms, is equivalent to (|𝑐|≥11)∧(|𝑑|≥7), since 𝑐 and 𝑑 are disjoint and so we may let 𝑥 be the appropriate part of 𝑐 and a suitable piece of 𝑑. The only remaining complication concerns instances of the term 𝑥 −(𝑥1 ∪⋯ ∪𝑥𝑁). But for these, the thing to notice is that any single positive size assertion about this term is realizable in our theory, since we have assumed that the lattice is unbounded, and so there will always be as many atoms as desired disjoint from any finite list of objects. But we must again pay attention to whether the requirements expressed by distinct clauses are contradictory.

Altogether, I have provided a procedure for eliminating quantifiers from any assertion in the language of locally Boolean lattices, down to the language augmented by unary predicates expressing the size of an object. This procedure works in any unbounded atomic locally Boolean lattice, and so the theorem is proved. QED

Corollary. The theory of unbounded atomic locally Boolean lattices is complete.

Proof. Every sentence in this theory is equivalent by the procedure to a quantifier-free sentence in the stated language. But since such sentences have no variables, they must simply be a Boolean combination of trivial size assertions about 0, such as (|0| ≥2) ∨¬(|0| =5), whose truth value is settled by the theory. QED

Corollary. The structure of hereditarily finite sets ⟨HF, ⊆⟩ is an elementary substructure of the entire set-theoretic universe ⟨𝑉, ⊆⟩, with the inclusion relation.

Proof. These structures are both unbounded atomic locally Boolean lattices, and so they each support the quantifier-elimination procedure. But they agree on the truth of any quantifier-free assertion about the sizes of hereditarily finite sets, and so they they must agree on all truth assertions about objects in HF. QED

Corollary. The structure ⟨𝑉, ⊆⟩ has a decidable theory. The structure ⟨HF, ⊆⟩ has a decidable elementary diagram, and hence a computably decidable presentation.

Proof. The theory is the theory of unbounded atomic locally Boolean lattices. Since the structure ⟨HF, ⊆⟩ has a computable presentation via the Ackerman coding of hereditarily finite sets, for which the subset relation and the size relations are computable, it follows that we may also compute the truth of any formula by first reducing it to a quantifier-free assertions of those types. So this is a computably decidable presentation. QED