This will be a talk for the Journées sur les Arithmétiques Faibles – Weak Arithmetics Days conference, held in New York at the CUNY Graduate Center, July 7 – 9, 2015.

Abstract. I will discuss several fun theorems and folklore results illustrating that the satisfaction relation of first-order logic is less absolute than one might have expected. Two models of set theory, for example, can have the same natural numbers 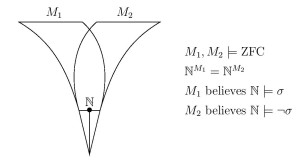$⟨\mathbb{N},+,\cdot ,0,1,<⟩$, yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree on whether it is a well-order and hence disagree about ${\omega }_1^{CK}$; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have a rank initial segment of the universe $⟨V_{\delta },\in ⟩$ in common, yet disagree about whether it is a model of ZFC. These theorems and others can be proved with elementary classical model-theoretic methods. On the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I have argued that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment.

Slides |  Main article: Satisfaction is not absolute