Mathematicians are deeply familiar with the complex number field , the algebraic closure of the real field , which can be constructed from by adjoining a new ideal element , the imaginary unit, and forming the complex numbers as formal pairs, defining the arithmetic subject to the rule . Thus we may add and multiply the complex numbers, according to the familiar rules:
The complex field thus provides a system of numbers giving sense to expressions like , while obeying the familiar algebraic rules of a field. Hamilton had presented this conception of complex numbers as pairs of real numbers to the Royal Irish Academy in 1833.
One may easily observe in the complex numbers, however, that is also a square root of , because
Thus, both and have the property of being square roots of , and indeed, these are the only square roots of in the complex field.
A small conundrum may arise when one realizes that therefore also fulfills what might have been taken as the “defining” property of the ideal element , namely, that it squares to . So this property doesn’t actually define , in light of the fact that there is another distinct object that also has this property. Can we tell and apart?
Not in the complex field, no, we cannot. The basic fact is that and are indiscernible as complex numbers with respect to the algebraic structure of —any property that has in the structure will also hold of . One way to see this is to observe that complex conjugation, the map is an automorphism of the complex number field, an isomorphism of the structure with itself. And since this automorphism swaps with , it follows that any statement true of in the complex numbers, expressible in the language of fields, will also hold of .
In fact, the complex number field has an extremely rich automorphism group, and every irrational complex number is indiscernible from various doppelgängers. There is an automorphism of that swaps and , for example, and another that permutes the cube roots of , mapping the real root with the two nonreal roots. So these numbers can have no property not shared by their various automorphic images. The general fact is that every complex number, except the rational numbers, is moved by some automorphism of . One can begin to see this by noticing that there are two ways to embed the algebraic field extensions into , and both embeddings extend fully to automorphisms of .
Because there is an automorphism of swapping and , it means that these two numbers are also indiscernible as complex numbers, just like and were—any property that holds in the complex numbers is also held by . But wait a minute, how can that be? After all, is positive and is negative, and isn’t this a property that separates them? Well, yes, in the real numbers this is a separating property, and since the order is definable from the algebraic structure of the real field (positive numbers are exactly the nonzero squares), it is a real algebraic property that distinguishes from , as only the former has itself a square root in . But this definition does not work in , since both have square roots there, and more generally, the surprise is that the real numbers are not definable as a subfield in the complex field —there is no property expressible in the language of fields that picks out exactly the real numbers. There are many distinct ways to embed as a subfield of , and none of them is definable in .
The conclusion is that if we regard the complex numbers with the field structure only, , then we cannot refer unambiguously to or , to or , or indeed to any irrational complex number. Every irrational number is moved by some automorphism of the complex field. The irrational algebraic numbers can be permuted in their finite sets of indiscernible roots of their irreducible polynomial, and any two transcendental complex numbers (transcendental over ) are automorphic. For example, there is an automorphism of moving to .
Finding a path out of that chaos, mathematicians like to conceive of as a field extension of , in effect fixing the copy of in . It is as though we are working in the structure , where we have augmented the complex field structure with a predicate picking out the real numbers. So this isn’t just a field, but a field with an identified subfield. In this structure, and and so on are definable, since one has identified the real numbers and within that subfield the order on the reals is definable, and so we can define every real algebraic number using this order. With the predicate for picking out the reals, the structure has only the one nontrivial automorphism, complex conjugation, and to my way of thinking, this is the reason that the indiscernibility issue is usually considered more prominently with and .
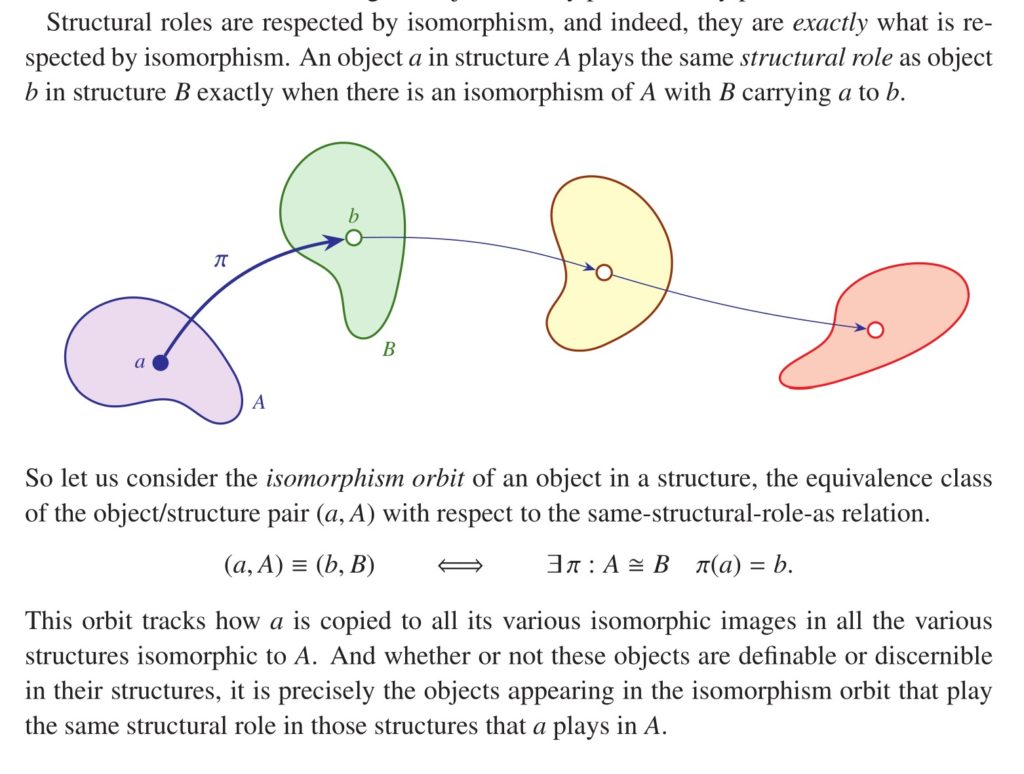
The indiscernibility of and in the complex field has been written on at length in the philosophical literature, since it seems to refute a certain philosophical account of structuralism that might otherwise have seemed appealing. Namely, the relevant view is a version of abstract structuralism, the view that what mathematical objects are is the structural role that they play in a mathematical system. On this view the natural number simply is the role that plays in Dedekind arithmetic, the role of being the successor of the successor of zero (Dedekind arithmetic is the categorical second-order axiomatization of ). The view is that what mathematical structure is is the structural roles that objects play in any instance of the structure. The structural role is exactly what is preserved by isomorphism, and so it would seem to be an invariant for the isomorphism orbits of an indidvidual with respect to a structure.
The problem with this version of abstract structuralism is that it seems to be refuted by the example of and in the complex field. Precisely because these numbers are automorphic, they would seem each to play exactly the same role in the complex field—the two numbers are isomorphic copies of one another via complex conjugation. Thus, they are distinct numbers, but play the same structural role, and so we cannot seem to identify the abstract number with the structural roles. This problem occurs, of course, in any mathematical structure that is not rigid.
The numbers and are indiscernible in the field structure of , but of course we can distinguish them in contexts with additional structure. For example, if we use the Hamilton presentation of the complex numbers as pairs of real numbers, representing with the pair , then the number has coordinates and has coordinates . The complex field equipped with this coordinate structure, perhaps given by the real and imaginary parts operators—let us call it the complex plane, as opposed to the complex field—is a rigid structure in which and are discernible and indeed definable.
Finally, this brings me to the main point of this blog post. What I would like to do is to prove that it is relatively consistent with ZFC that we can definably construct a copy of the complex numbers in such a way that not only are and indiscernible in the field structure, but actually the particular set-theoretic objects and are indiscernible in the set-theoretic background in which the construction is undertaken.
Goal. A definable copy of the complex field in which the two square roots of are indiscernible not only in the field structure, but also in the set-theoretic background in which the construction of the field takes place.
These two aims are in tension, for we want the particular copy to be definable (as a particular set-theoretic object, not just defined up to isomorphism), but the individual square roots of to be set-theoretically indiscernible.
The goal is not always possible. For example, some models of ZFC are pointwise definable, meaning that every individual set is definable in them by some distinguishing set-theoretic property. More generally, if the V=HOD axiom holds, then there is a definable global well order of the set-theoretic universe, and with any such order we could define a linear order on in any definable copy of , which would allow us to define each of the roots. For these reasons, in some models of ZFC, it is not possible to achieve the goal, and the most we can hope for a consistency result.
But indeed, the consistency goal is achievable.
Theorem. If ZFC is consistent, then there is a model of ZFC that has a definable complete ordered field with a definable algebraic closure , such that the two square roots of in are set-theoretically indiscernible, even with ordinal parameters.
Proof. The proof makes use of what are known as Grozek-Laver pairs, definable pair sets having no ordinal-definable element. See M. Groszek & R. Laver, Finite Groups of OD-conjugates, Periodica Mathematica Hungarica, v. 18, pp. 87–97 (1987), for a very general version of this. This theorem also appears at theorem 4.6 in my paper Ehrenfeucht’s lemma in set theory, joint with Gunter Fuchs, Victoria Gitman, and myself. The arguments provide a model of set theory with a definable pair set , such that neither element nor is definable from ordinal parameters. The pair set is definable, but neither element is definable.
To undertake the construction, we start with one of the standard definable constructions of the real field . For example, we could use Dedekind cuts in , where is constructed explicitly as the quotient field of the integer ring in some canonical definable manner, and where the integers are definably constructed from a definable copy of the natural numbers , such as the finite von Neumann ordinals. So we have a definable complete ordered field, the real field .
Given this and the set , we follow a suggestion of Timothy Gowers in the discussion of this problem on Twitter. Namely, we use the elements of as variables to form the polynomial ring , meaning , where and are the two elements of . It is not necessary to distinguish the elements of to form this ring of polynomials, since we take all finite polynomial expressions using real coefficients and elements of raised to a power. (In particular, although I have referred to the elements as and , there is to be no suggestion that I am somehow saying is the “real” ; I am not, for I could have called them , or , or ,, and so on.) Then we quotient by the ideal , which is defined symmetrically in the elements of , since it is the same ideal as . Let be the quotient , which will make both and the two square roots of , and so by the fundamental theorem of algebra this is a copy of the complex numbers.
Since and were definable, and we didn’t need ever to choose a particular element of in the construction to define the polynomial ring or the ideal, this copy of is definable without parameters. But since and are set-theoretically indiscernible in the model of set theory in which we are undertaking the construction, it follows that their equivalence classes in the quotient are also indiscernible. And so we have a definable copy of the complex field , extending a definable copy of , in which the two square roots of are indiscernible not just in the field structure, but fully in the set-theoretic background in which the fields were constructed.
In particular, in this model of set theory, there will be absolutely no way to distinguish the two roots by any further definable structure, whether using second-order or higher-order definitions of the field or using any definable set-theoretic property whatsoever.
The analysis suggests a natural further inquiry. Namely,
Question. Is there a model of set theory with a definable copy of the complex field , such that the hierarchy of relative definability and indiscernibility in matches the set-theoretic relative definability and indiscernibility of the objects?
That is, we would want to mimic the phenomenon of and in the above construction with all complex numbers, so that and were also indiscernible, not just in this copy of but also in the set-theoretic background, and was set-theoretically indiscernible from the other new fourth-root of , but can set-theoretically define both and . In other words, I want the set-theoretic definability hierarchy to match the complex-number-theoretic definability hierarchy. I may post this question on MathOverflow, when I formulate a version of it with which I am satisfied. I believe it will be answered by iterated Sacks forcing in a manner similar to that used in many papers by Marcia Groszek, and in particular, in my paper with her, The Implicitly constructible universe.