Transfinite game values in infinite chess and other infinite games, Hausdorff Center, Bonn, May 2014

Posted on March 15, 2014 by Joel David Hamkins

I shall be very pleased to speak at the colloquium and workshop Infinity, computability, and metamathematics, celebrating the 60th birthdays of Peter Koepke and Philip Welch, held at the Hausdorff Center for Mathematics May 23-25, 2014 at the Universität Bonn. My talk will be the Friday colloquium talk, for a general mathematical audience.

Abstract. I shall give a general introduction to the theory of infinite games, using infinite chess—chess played on an infinite edgeless chessboard—as a central example. Since chess, when won, is won at a finite stage of play, infinite chess is an example of what is known technically as an open game, and such games admit the theory of transfinite ordinal game values. I shall exhibit several interesting positions in infinite chess with very high transfinite game values. The precise value of the omega one of chess is an open mathematical question.

Slides | Schedule | Transfinite game values in infinite chess | The mate-in-n problem of infinite chess is decidable

Strongly uplifting cardinals and the boldface resurrection axioms

Posted on March 12, 2014 by Joel David Hamkins

[bibtex key=HamkinsJohnstone2017:StronglyUpliftingCardinalsAndBoldfaceResurrection]

Abstract. We introduce the strongly uplifting cardinals, which are equivalently characterized, we prove, as the superstrongly unfoldable cardinals and also as the almost hugely unfoldable cardinals, and we show that their existence is equiconsistent over ZFC with natural instances of the boldface resurrection axiom, such as the boldface resurrection axiom for proper forcing.

The strongly uplifting cardinals, which we introduce in this article, are a boldface analogue of the uplifting cardinals introduced in our previous paper, Resurrection axioms and uplifting cardinals, and are equivalently characterized as the superstrongly unfoldable cardinals and also as the almost hugely unfoldable cardinals. In consistency strength, these new large cardinals lie strictly above the weakly compact, totally indescribable and strongly unfoldable cardinals and strictly below the subtle cardinals, which in turn are weaker in consistency than the existence of $0 ♯$ . The robust diversity of equivalent characterizations of this new large cardinal concept enables constructions and techniques from much larger large cardinal contexts, such as Laver functions and forcing iterations with applications to forcing axioms. Using such methods, we prove that the existence of a strongly uplifting cardinal (or equivalently, a superstrongly unfoldable or almost hugely unfoldable cardinal) is equiconsistent over ZFC with natural instances of the boldface resurrection axioms, including the boldface resurrection axiom for proper forcing, for semi-proper forcing, for c.c.c. forcing and others. Thus, whereas in our prior article we proved that the existence of a mere uplifting cardinal is equiconsistent with natural instances of the (lightface) resurrection axioms, here we adapt both of these notions to the boldface context.

Definitions.

An inaccessible cardinal $𝜅$ is strongly uplifting if for every ordinal $𝜃$ it is strongly $𝜃$ -uplifting, which is to say that for every $𝐴 \subset 𝑉 𝜅$ there is an inaccessible cardinal $𝛾 \geq 𝜃$ and a set $𝐴 * \subset 𝑉 𝛾$ such that $⟨ 𝑉 𝜅, \in, 𝐴 ⟩ ≺ ⟨ 𝑉 𝛾, \in, 𝐴 * ⟩$ is a proper elementary extension.
A cardinal $𝜅$ is superstrongly unfoldable, if for every ordinal $𝜃$ it is superstrongly $𝜃$ -unfoldable, which is to say that for each $𝐴 \in 𝐻 𝜅 +$ there is a $𝜅$ -model $𝑀$ with $𝐴 \in 𝑀$ and a transitive set $𝑁$ with an elementary embedding $𝑗 : 𝑀 \to 𝑁$ with critical point $𝜅$ and $𝑗 (𝜅) \geq 𝜃$ and $𝑉 𝑗 (𝜅) \subset 𝑁$ .
A cardinal $𝜅$ is almost-hugely unfoldable, if for every ordinal $𝜃$ it is almost-hugely $𝜃$ -unfoldable, which is to say that for each $𝐴 \in 𝐻 𝜅 +$ there is a $𝜅$ -model $𝑀$ with $𝐴 \in 𝑀$ and a transitive set $𝑁$ with an elementary embedding $𝑗 : 𝑀 \to 𝑁$ with critical point $𝜅$ and $𝑗 (𝜅) \geq 𝜃$ and $𝑁 < 𝑗 (𝜅) \subset 𝑁$ .

Remarkably, these different-seeming large cardinal concepts turn out to be exactly equivalent to one another. A cardinal $𝜅$ is strongly uplifting if and only if it is superstrongly unfoldable, if and only if it is almost hugely unfoldable. Furthermore, we prove that the existence of such a cardinal is equiconsistent with several natural instances of the boldface resurrection axiom.

Theorem. The following theories are equiconsistent over ZFC.

There is a strongly uplifting cardinal.
There is a superstrongly unfoldable cardinal.
There is an almost hugely unfoldable cardinal.
The boldface resurrection axiom for all forcing.
The boldface resurrection axiom for proper forcing.
The boldface resurrection axiom for semi-proper forcing.
The boldface resurrection axiom for c.c.c. forcing.
The weak boldface resurrection axiom for countably-closed forcing, axiom-A forcing, proper forcing and semi-proper forcing, plus $\neg C H$ .

Large cardinals need not be large in HOD, Rutgers logic seminar, April 2014

Posted on March 3, 2014 by Joel David Hamkins

I shall speak at the Rutgers Logic Seminar on April 21, 2014, 5:00-6:20 pm, Room 705, Hill Center, Busch Campus, Rutgers University.

Abstract. I will show that large cardinals, such as measurable, strong and supercompact cardinals, need not exhibit their large cardinal nature in HOD. Specifically, it is relatively consistent that a supercompact cardinal is not weakly compact in HOD, and one may construct models with a proper class of supercompact cardinals, none of them weakly compact in HOD. This is current joint work with Cheng Yong.

Article

Kelley-Morse set theory implies Con(ZFC) and much more

Posted on February 13, 2014 by Joel David Hamkins

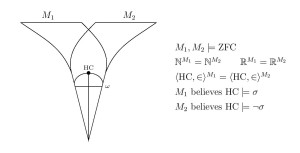
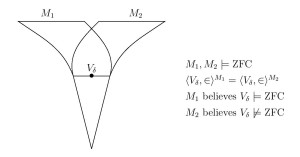
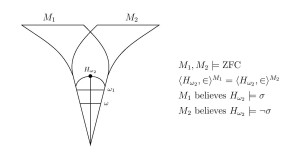
I should like to give a brief account of the argument that KM implies Con(ZFC) and much more. This argument is well-known classically, but unfortunately seems not to be covered in several of the common set-theoretic texts.

First, without giving a full formal axiomatization, let us review a little what KM is. (And please see Victoria Gitman’s post on variant axiomatizations of KM.) In contrast to Zermelo-Frankael (ZFC) set theory, which has a purely first-order axiomatization, both Kelley-Morse (KM) set theory and Gödel-Bernays (GBC) set theory are formalized in the second-order language of set theory, where we have two sorts of objects, namely sets and classes, in addition to the usual set membership relation $\in$ . A model of KM will have the form $⟨ 𝑀, \in 𝑀, 𝑆 ⟩$ , where $𝑀$ is the collection of sets in the model, and $𝑆$ is a collection of classes in the model; each class $𝐴 \in 𝑆$ is simply the subset of $𝑀$ . Both KM and GBC will imply that $⟨ 𝑀, \in 𝑀 ⟩$ is a model of ZFC. Both GBC and KM assert the global choice principle, which asserts that there is a class that is a well-ordering of all the sets (or equivalently that there is a class bijection of all the sets with the class of ordinals). Beyond this, both GBC and KM have a class comprehension principle, asserting that for certain formulas $𝜑$ , having finitely many set and class parameters, that ${𝑥 ∣ 𝜑 (𝑥)}$ forms a class. In the case of GBC, we have this axiom only for $𝜑$ having only set quantifiers, but in KM we also allow formulas $𝜑$ that have quantification over classes (which are interpreted in the model by quanfying over $𝑆$ ). Both theories also assert that the intersection of a class with a set is a set (which amounts to the separation axiom, and this follows from replacement anyway). In addition, both GBC and KM have a replacement axiom, asserting that if $𝑢$ is a set, and for every $𝑎 \in 𝑢$ there is a unique set $𝑏$ for which $𝜑 (𝑎, 𝑏)$ , where $𝜑$ has finitely many class and set parameters, then ${𝑏 ∣ \exists 𝑎 \in 𝑢 𝜑 (𝑎, 𝑏)}$ is a set. In the case of GBC, we have the replacement axiom only when all the quantifiers of $𝜑$ are first-order quantifiers only, quantifying only over sets, but in KM we allow $𝜑$ to have second-order quantifiers. Thus, both GBC and KM can be thought of as rather direct extensions of ZFC to the second-order class context, but KM goes a bit further by applying the ZFC axioms also in the case of the new second-order properties that become available in that context, while GBC does not.

The theorem I want to discuss is:

Theorem. KM proves Con(ZFC).

Indeed, ultimately we’ll show in KM that there is transitive model of ZFC, and furthermore that the universe $𝑉$ is the union of an elementary chain of elementary rank initial segments $𝑉 𝜃 ≺ 𝑉$ , each of which, in particular, is a transitive model of ZFC.

We’ll prove it in several steps, which will ultimately reveal stronger results and a general coherent method and idea.

KM has a truth predicate for first-order truth. The first step is to argue in KM that there is a truth predicate Tr for first-order truth, a class of pairs $(𝜑, 𝑎)$ , where $𝜑$ is a first-order formula in the language of set theory and $𝑎$ is an assignment of the free variabes of $𝜑$ to particular sets, such that the class Tr gets the right answer on the quantifier-free formulas and obeys the recursive Tarskian truth conditions for Boolean combinations and first-order quantification, that is, the conditions explaining how the truth of a formula is determined from the truth of its immediate subformulas.

To construct the truth predicate, begin with the observation that we may easily define, even in ZFC, a truth predicate for quantifier-free truth, and indeed, even first-order $Σ 𝑛$ truth is $Σ 𝑛$ -definable, for any meta-theoretic natural number $𝑛$ . In KM, we may consider the set of natural numbers $𝑛$ for which there is a partial truth predicate $𝑇$ , one which is defined only for first-order formulas of complexity at most $Σ 𝑛$ , but which gives the correct answers on the quantifier-free formulas and which obeys the Tarskian conditions up to complexity $Σ 𝑛$ . The set of such $𝑛$ exists, by the separation axiom of KM, since we can define it by a property in the second-order language (this would not work in GBC, since there is a second-order quantifier asking for the existence of the partial truth predicate). But now we simply observe that the set contains $𝑛 = 0$ , and if it contains $𝑛$ , then it contains $𝑛 + 1$ , since from any $Σ 𝑛$ partial truth predicate we can define one for $Σ 𝑛 + 1$ . So by induction, we must have such truth predicates for all natural numbers $𝑛$ . This inductive argument really used the power of KM, and cannot in general be carried out in GBC or in ZFC.

A similar argument shows by induction that all these truth predicates must agree with one another, since there can be no least complexity stage where they disagree, as the truth values at that stage are completely determined via the Tarski truth conditions from the earlier stage. So in KM, we have a unique truth predicate defined on all first-order assertions, which has the correct truth values for quantifier-free truth and which obeys the Tarskian truth conditions.

The truth predicate Tr agrees with actual truth on any particular assertion. Since the truth predicate Tr agrees with the actual truth of quantifier-free assertions and obeys the Tarskian truth conditions, it follows by induction in the meta-theory (and so this is a scheme of assertions) that the truth predicate that we have constructed agrees with actual truth for any meta-theoretically finite assertion.

The truth predicate Tr thinks that all the ZFC axioms are all true. Here, we refer not just to the truth of actual ZFC axioms (which Tr asserts as true by the previous paragraph), but to the possibly nonstandard formulas that exist inside our KM universe. We claim nevertheless that all such formulas the correspond to an axiom of ZFC are still decreed true by the predicate Tr. We get all the easy axioms by the previous paragraph, since those axioms are true under KM. It remains only to verify that Tr asserts as true all instances of the replacement axiom. For this, suppose that there is a set $𝑢$ , such that Tr thinks every $𝑎 \in 𝑢$ has a unique $𝑏$ for which Tr thinks $𝜑 (𝑎, 𝑏)$ . But now by KM (actually we need only GB here), we may apply the replacement axiom with Tr a predicate, to find that ${𝑏 ∣ \exists 𝑎 \in 𝑢 T r t h i n k s t h a t 𝜑 (𝑎, 𝑏)}$ is a set, whether or not $𝜑$ is an actual finite length formula in the metatheory. It follows that Tr will assert this instance of replacement, and so Tr will decree all instances of replacement as being true.

KM produces a closed unbounded tower of transitive models of ZFC. This is the semantic approach, which realizes the universe as the union of an elementary chain of elementary substructures $𝑉 𝜃$ . Namely, by the reflection theorem, there is a closed unbounded class of ordinals $𝜃$ such that $⟨ 𝑉 𝜃, \in, T r \cap 𝑉 𝜃 ⟩ ≺ Σ 1 ⟨ 𝑉, \in, T r ⟩$ . (We could have used $Σ 2$ or $Σ 17$ here just as well.) It follows that $T r \cap 𝑉 𝜃$ fulfills the Tarskian truth conditions on the structure $⟨ 𝑉 𝜃, \in ⟩$ , and therefore agrees with the satisfaction in that structure. It follows that $𝑉 𝜃 ≺ 𝑉$ for first-order truth, and since ZFC was part of what is asserted by Tr, we have produced here a transitive model of ZFC. More than this, what we have is a closed unbounded class of ordinals $𝜃$ , which form an elementary chain $𝑉 𝜃 0 ≺ 𝑉 𝜃 1 ≺ \dots ≺ 𝑉 𝜆 ≺ \dots,$ whose union is the entire universe. Each set in this chain is a transitive model of ZFC and much more.

An alternative syntactic approach. We could alternatively have reasoned directly with the truth predicate as follows. First, the truth predicate is complete, and contains no contradictions, simply because part of the Tarskian truth conditions are that $\neg 𝜑$ is true according to Tr if and only if $𝜑$ is not true according to Tr, and this prevents explicit contradictions from ever becoming true in Tr, while also ensuring completeness. Secondly, the truth predicate is closed under deduction, by a simple induction on the length of the proof. One must verify that certain logical validities are decreed true by Tr, and then it follows easily from the truth conditions that Tr is closed under modus ponens. The conclusion is that the theory asserted by Tr contains ZFC and is consistent, so Con(ZFC) holds. Even though Tr is a proper class, the set of sentences it thinks are true is a complete consistent extension of ZFC, and so Con(ZFC) holds. QED

The argument already shows much more than merely Con(ZFC), for we have produced a proper class length elementary tower of transitive models of ZFC. But it generalizes even further, for example, by accommodating class parameters. For any class $𝐴$ , we can construct in the same way a truth predicate $T r 𝐴$ for truth in the first-order language of set theory augmented with a predicate for the class $𝐴$ .

In particular, KM proves that there is a truth predicate for truth-about-truth, that is, for truth-about-Tr, and for truth-about-truth-about-truth, and so on, iterating quite a long way. (Of course, this was also clear directly from the elementary tower of transitive models.)

The elementary tower of transitive elementary rank initial segments $𝑉 𝜃 ≺ 𝑉$ surely addresses what is often seen as an irritating limitation of the usual reflection theorem in ZFC, that one gets only $Σ 𝑛$ -reflection $𝑉 𝜃 ≺ Σ 𝑛 𝑉$ rather than this kind of full reflection, which is what one really wants in a reflection theorem. The point is that in KM we are able to refer to our first-order truth predicate Tr and overcome that restriction.

Doesn’t the existence of a truth predicate violate Tarski’s theorem on the non-definability of truth? No, not here, since the truth predicate Tr is not definable in the first-order language of set theory. Tarski’s theorem asserts that there can be no definable class (even definable with set parameters) that agrees with actual truth on quantifier-free assertions and which satisfies the recursive Tarskian truth conditions. But nothing prevents having some non-definable class that is such a truth predicate, and that is our situation here in KM.

Although the arguments here show that KM is strictly stronger than ZFC in consistency strength, it is not really very much stronger, since if $𝜅$ is an inaccessible cardinal, then it is not difficult to argue in ZFC that $⟨ 𝑉 𝜅, \in, 𝑉 𝜅 + 1 ⟩$ is a model of KM. Indeed, there will be many smaller models of KM, and so the consistency strength of KM lies strictly between that of ZFC, above much of the iterated consistency hierarchy, but below that of ZFC plus an inaccessible cardinal.

Large cardinals need not be large in HOD, CUNY Set Theory Seminar, January 2014

Posted on January 24, 2014 by Joel David Hamkins

This will be a talk for the CUNY Set Theory Seminar, January 31, 2014, 10:00 am.

Abstract. I will demonstrate that a large cardinal need not exhibit its large cardinal nature in HOD. I will begin with the example of a measurable cardinal that is not measurable in HOD. After this, I will describe how to force a more extreme divergence. For example, among other possibilities, it is relatively consistent that there is a supercompact cardinal that is not weakly compact in HOD. This is very recent joint work with Cheng Yong.

Article

Superstrong and other large cardinals are never Laver indestructible, ASL 2014, Boulder, May 2014

Posted on January 22, 2014 by Joel David Hamkins

This will be an invited talk at the ASL 2014 North American Annual Meeting (May 19-22, 2014) in the special session Set Theory in Honor of Rich Laver, organized by Bill Mitchell and Jean Larson.

Abstract. The large cardinal indestructibility phenomenon, discovered by Richard Laver with his seminal result on supercompact cardinals, is by now often seen as pervasive in the large cardinal hierarchy. Nevertheless, a new never-indestrucible phenomenon has emerged. Superstrong cardinals, for example, are never Laver indestructible. Similarly, almost huge cardinals, huge cardinals, superhuge cardinals, rank-into-rank cardinals, extendible cardinals, 1-extendible cardinals, 0-extendible cardinals, weakly superstrong cardinals, uplifting cardinals, pseudo-uplifting cardinals, superstrongly unfoldable cardinals, $Σ 𝑛$ -reflecting cardinals, $Σ 𝑛$ -correct cardinals and $Σ 𝑛$ -extendible cardinals (all for $𝑛 \geq 3$ ) are never Laver indestructible. The proof involves a detailed technical analysis of the complexity of the definition in Laver’s theorem on the definability of the ground model, thereby involving and extending results in set-theoretic geology. This is joint work between myself and Joan Bagaria, Kostas Tasprounis and Toshimichi Usuba.

Article | Slides

Universal structures, GC MathFest, February 2014

Posted on January 18, 2014 by Joel David Hamkins

This will be a talk for the CUNY Graduate Center MathFest, held on the afternoon of Februrary 4, 2014, intended for graduate-school-bound undergraduate students, including prospective students for the CUNY Graduate Center, giving them a chance to meet graduate students and faculty at the CUNY Graduate Center and see the kind of mathematics that is done here.

In this 30 minute talk, I’ll introduce the concept of a universal structure, with various examples, including the countable random graph, the surreal number line and the hypnagogic digraph.

MathFest Program/schedule

Satisfaction is not absolute, Dartmouth Logic Seminar, January 2014

Posted on January 4, 2014 by Joel David Hamkins

This will be a talk for the Dartmouth Logic Seminar on January 23rd, 2014.

Abstract. I will discuss a number of theorems showing that the satisfaction relation of first-order logic is less absolute than might have been supposed. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic $⟨ ℕ, +, \cdot, 0, 1, < ⟩$ , yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree on whether it is a well-order; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have a rank initial segment of the universe $⟨ 𝑉 𝛿, \in ⟩$ in common, yet disagree about whether it is a model of ZFC. The theorems are proved with elementary classical model-theoretic methods, and many of them can be considered folklore results in the subject of models of arithmetic.

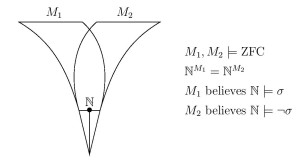Indefinite arithmetic truth On the basis of these mathematical results, Ruizhi Yang (Fudan University, Shanghai) and I have argued that the definiteness of truth in a structure, such as with arithmetic truth in the standard model of arithmetic, cannot arise solely from the definiteness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.

Main article: Satisfaction is not absolute

Infinite chess and the theory of infinite games, Dartmouth Mathematics Colloquium, January 2014

Posted on January 4, 2014 by Joel David Hamkins

This will be a talk for the Dartmouth Mathematics Colloquium on January 23rd, 2014.

Abstract. Using infinite chess as a central example—chess played on an infinite edgeless board—I shall give a general introduction to the theory of infinite games. Infinite chess is an example of what is called an open game, a potentially infinite game which when won is won at a finite stage of play, and every open game admits the theory of transfinite ordinal game values. These values provide a measure of the distance remaining to an actual victory, and when they are known, the game values provide a canonical winning strategy for the winning player. I shall exhibit

several interesting positions in infinite chess with high transfinite game values. The precise value of the omega one of chess, however, the supremum of all such ordinal game values, is an open mathematical question; in the case of infinite three-dimensional chess, meanwhile, Evans and I have proved that every countable ordinal arises as a game value. Infinite chess also illustrates an interesting engagement with computability issues. For example, there are computable infinite positions in infinite chess that are winning for white, provided that the players play according to a computable procedure of their own choosing, but which is no longer winning for white when non-computable play is allowed. Also, the mate-in-n problem for finite positions in infinite chess is computably decidable (joint work with Schlicht, Brumleve and myself), despite the high quantifier complexity of any straightforward representation of it. The talk will be generally accessible for mathematicians, particularly those with at least rudimentary knowledge of ordinals and of chess.

Poster | Slides (8mb) | Transfinite game values in infinite chess | The mate-in-n problem of infinite chess is decidable

Satisfaction is not absolute

Posted on December 3, 2013 by Joel David Hamkins

[bibtex key=HamkinsYang:SatisfactionIsNotAbsolute]

Abstract. We prove that the satisfaction relation $N ⊧ 𝜑 [⃗ 𝑎]$ of first-order logic is not absolute between models of set theory having the structure $N$ and the formulas $𝜑$ all in common. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic $⟨ ℕ, +, \cdot, 0, 1, < ⟩$ , yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and the same arithmetic truths, yet disagree on their truths-about-truth, at any desired level of the iterated truth-predicate hierarchy; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have the same $⟨ 𝐻 𝜔 2, \in ⟩$ or the same rank-initial segment $⟨ 𝑉 𝛿, \in ⟩$ , yet disagree on which assertions are true in these structures.

On the basis of these mathematical results, we argue that a philosophical commitment to the determinateness of the theory of truth for a structure cannot be seen as a consequence solely of the determinateness of the structure in which that truth resides. The determinate nature of arithmetic truth, for example, is not a consequence of the determinate nature of the arithmetic structure $ℕ = {0, 1, 2, \dots}$ itself, but rather, we argue, is an additional higher-order commitment requiring its own analysis and justification.

Many mathematicians and philosophers regard the natural numbers $0, 1, 2, \dots$ , along with their usual arithmetic structure, as having a privileged mathematical existence, a Platonic realm in which assertions have definite, absolute truth values, independently of our ability to prove or discover them. Although there are some arithmetic assertions that we can neither prove nor refute—such as the consistency of the background theory in which we undertake our proofs—the view is that nevertheless there is a fact of the matter about whether any such arithmetic statement is true or false in the intended interpretation. The definite nature of arithmetic truth is often seen as a consequence of the definiteness of the structure of arithmetic $⟨ ℕ, +, \cdot, 0, 1, < ⟩$ itself, for if the natural numbers exist in a clear and distinct totality in a way that is unambiguous and absolute, then (on this view) the first-order theory of truth residing in that structure—arithmetic truth—is similarly clear and distinct.

Feferman provides an instance of this perspective when he writes (Feferman 2013, Comments for EFI Workshop, p. 6-7) :

In my view, the conception [of the bare structure of the natural numbers] is completely clear, and thence all arithmetical statements are definite.

It is Feferman’s `thence’ to which we call attention. Martin makes a similar point (Martin, 2012, Completeness or incompleteness of basic mathematical concepts):

What I am suggesting is that the real reason for confidence in first-order completeness is our confidence in the full determinateness of the concept of the natural numbers.

Many mathematicians and philosophers seem to share this perspective. The truth of an arithmetic statement, to be sure, does seem to depend entirely on the structure $⟨ ℕ, +, \cdot, 0, 1, < ⟩$ , with all quantifiers restricted to $ℕ$ and using only those arithmetic operations and relations, and so if that structure has a definite nature, then it would seem that the truth of the statement should be similarly definite.

Nevertheless, in this article we should like to tease apart these two ontological commitments, arguing that the definiteness of truth for a given mathematical structure, such as the natural numbers, the reals or higher-order structures such as $𝐻 𝜔 2$ or $𝑉 𝛿$ , does not follow from the definite nature of the underlying structure in which that truth resides. Rather, we argue that the commitment to a theory of truth for a structure is a higher-order ontological commitment, going strictly beyond the commitment to a definite nature for the underlying structure itself.

We make our argument in part by proving that different models of set theory can have a structure identically in common, even the natural numbers, yet disagree on the theory of truth for that structure.

Theorem.

Two models of set theory can have the same structure of arithmetic $⟨ ℕ, +, \cdot, 0, 1, < ⟩ 𝑀 1 = ⟨ ℕ, +, \cdot, 0, 1, < ⟩ 𝑀 2,$ yet disagree on the theory of arithmetic truth.
Two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree about whether it is a well-order.
Two models of set theory that have the same natural numbers and the same reals, yet disagree on projective truth.
Two models of set theory can have a transitive rank initial segment in common $⟨ 𝑉 𝛿, \in ⟩ 𝑀 1 = ⟨ 𝑉 𝛿, \in ⟩ 𝑀 2,$ yet disagree about whether it is a model of ZFC.

The proofs use only elementary classical methods, and might be considered to be a part of the folklore of the subject of models of arithmetic. The paper includes many further examples of the phenomenon, and concludes with a philosophical discussion of the issue of definiteness, concerning the question of whether one may deduce definiteness-of-truth from definiteness-of-objects and definiteness-of-structure.

The foundation axiom and elementary self-embeddings of the universe

Posted on November 4, 2013 by Joel David Hamkins

[bibtex key=DaghighiGolshaniHaminsJerabek2013:TheFoundationAxiomAndElementarySelfEmbeddingsOfTheUniverse]

In this article, we examine the role played by the axiom of foundation in the well-known Kunen inconsistency, the theorem asserting that there is no nontrivial elementary embedding of the set-theoretic universe to itself. All the standard proofs of the Kunen inconsistency make use of the axiom of foundation (see Kanamori’s books and also Generalizations of the Kunen inconsistency), and this use is essential, assuming that $Z F C$ is consistent, because as we shall show there are models of $Z F C - f$ that admit nontrivial elementary self-embeddings and even nontrivial definable automorphisms. Meanwhile, a fragment of the Kunen inconsistency survives without foundation as the claim in $Z F C - f$ that there is no nontrivial elementary self-embedding of the class of well-founded sets. Nevertheless, some of the commonly considered anti-foundational theories, such as the Boffa theory $B A F A$ , prove outright the existence of nontrivial automorphisms of the set-theoretic universe, thereby refuting the Kunen assertion in these theories. On the other hand, several other common anti-foundational theories, such as Aczel’s anti-foundational theory $Z F C - f + A F A$ and Scott’s theory $Z F C - f + S A F A$ , reach the opposite conclusion by proving that there are no nontrivial elementary embeddings from the set-theoretic universe to itself. Our summary conclusion, therefore, is that the resolution of the Kunen inconsistency in set theory without foundation depends on the specific nature of one’s anti-foundational stance.

This is joint work with Ali Sadegh Daghighi, Mohammad Golshani, myself and Emil Jeřábek, which grew out of our interaction on Ali’s question on MathOverflow, Is there any large cardinal beyond the Kunen inconsistency?

Just do it? Barbara Gail Montero interviewed on The Philosopher's Zone

Posted on November 3, 2013 by Joel David Hamkins

Barbara’s radio interview this week on Radio National:

Just do it?

November 3, 2013
BARBARA GAIL MONTERO interviewed by Joe Gelonesi along with Richard Menary on The Philosopher’s Zone.

Famed choreographer George Balanchine was reputed to have said, “don’t think, dear: just do”. The idea that champion performers switch off their brains to achieve their best has taken hold in popular imagination. Just do it promises an existential zone where real players hit the heights whilst the rest shuffle to the back of the pack. We explore Expert action, a philosophical football punted between those for automatic responses and those who hear the whirring cogs.

→ go listen to `Just Do It‘

Barbara was previously interviewed on Leading Minds, with David Brendel.

Rubik's cube competition, CSI, November 14, 2013

Posted on October 24, 2013 by Joel David Hamkins

Come and compete in the CSI Rubik’s cube competition!

November 14, 2013, College of Staten Island of CUNY, 1S-107, 2:30 pm.

Sponsored by MTH 339, and the CSI Math Club.

As a part of the undergraduate course in abstract algebra (MTH 339), which I am teaching this semester at the College of Staten Island, we shall hold a Rubik’s cube competition on November 14th. In class, I have used the Rubik’s cube as a source of examples to explain various group-theoretic concepts, and I have encouraged the students to learn to solve the cube. Several have now already mastered it, and there seems lately to be a lot of Rubik’s cube activity in the math department. (I am giving extra credit for any student who can solve a scrambled cube in my office.)

Several students have learned how to solve the cube from the following video, which explains one of the layer-based solution methods:

Free New York Pizza!

The Competition. On November 14, 2013, we will have the Rubik’s cube competition, with several rounds of competition, to see who can solve the cube the fastest. Prizes will be awarded, and best of all, there will be free pizza!

Results Of the Competition

The event has now taken place. We had 15 competitors, from all around the College and beyond. We organized two qualifying heats of 7 and 8 competitors, respectively, taking the top four from each qualtifying heat to form the quarterfinalist competitors. The top four of these formed the semifinalist competitors. And the top two of these headed off in the championship round. The champion, Sam Obisanya, won all the rounds in which he competed, and his cube was a blaze of lightning color as he solved it. Honorable mention goes especially to Oveen Joseph, who faced Sam in the championship round and who came out to the college from middle school I.S.72, where he is in the 7th grade, and also to Justin Mills, who had extremely fast times.

Quarterfinals:

Itiel Cohen (CSI math major)

William George (CSI math major)

Oveen Joseph (middle school I.S.72, 7th grade)

Wing Yang Law (CSI math major)

Justin Mills (CSI psychology major)

Mike Siozios (CSI math major)

Sam Obisanya (CSI nursing major)

James Yap (CSI math major)

Semifinals:

Oveen Joseph

Justin Mills

Sam Obisanya

James Yap

Championship round:

Oveen Joseph

Sam Obisanya

Final Champion:

Sam Obisanya

Congratulations to our champion and to all the competitors.

Rubik's cube

Win the game of Nim! CSI Math Club, October, 2013

Posted on October 24, 2013 by Joel David Hamkins

This will be a talk for the CSI Math Club on October 31, 2013 at 2:30 pm in room 1S-107.

Abstract Come and learn how to play and win the game of Nim! The game has two players, faced with several small piles of blocks. Each player, on their turn, can remove one or more blocks from one pile, but only one pile. (Removing a whole pile is fine.) The player who removes the last block wins. This simple-to-describe game is maddening for those who don’t know the secret mathematical winning strategy. Come and learn the mathematical secret that will allow you to win every time against someone who doesn’t know it.

Doubled, squared, cubed: a math game for kids or anyone

Posted on October 21, 2013 by Joel David Hamkins

The number that must not be named

Doubled, squared, cubed is a great math game to play with kids or anyone interested in math. It is a talking game, requiring no pieces or physical objects, played by a group of two or more people at almost any level of mathematical difficulty, while sitting, walking, boating or whatever. We play it in our family (two kids, ages 7 and 11) when we are sitting around a table or when walking somewhere or when traveling by train. I fondly recall playing the game with my brothers and sisters in my own childhood.

The game proceeds by first agreeing on an allowed number range. For youngsters, perhaps one wants to allow the integers from 0 to 100, inclusive, but one will want to have negative numbers soon enough, and of course much more sophisticated play is possible. Eventually, one lessens or even abandons the restriction altogether. The first player offers a number, and each subsequent player in turn offers a mathematical operation, which is to be applied to the current number, which must not be mentioned explicitly. The resulting number must be in the allowed number range.

The goal of the game is successfully to keep track of the number as it changes, and to offer an operation that makes sense with that number, while staying within the range of allowed numbers. The point is to have some style, to offer an operation that proves that you know what the number is, without stating the number explicitly. Perhaps your operation makes the new number a nice round number, or perhaps your operation can seldom be legally applied, and so applying it indicates that you know it is allowed to do so. You must offer only operations that you yourself can compute, and which do not rely on hidden information (for example, “times the number of grapes I ate at breakfast” is not really permissible).

A losing move is one that doesn’t make sense or that results in a number outside the allowed range. In this case, the game can continue without that person, and the last person left wins. It is not allowed to offer an operation that can always be applied, such as “times zero” or “minus itself“, or which can always be applied immediately after the previous operation, such as saying “times two” right after someone said, “cut in half”. But in truth, the main point is to have some fun, rather than to win. Part of the game is surely simply to talk about new mathematical operations, and we usually take time out to discuss or explain any mathematical issue that may come up. So this is an enjoyable way for the kids to encounter new mathematical ideas.

Let me simply illustrate a typical progression of the game, as it might be played in my family:

Hypatia: one

Barbara: doubled

Horatio: squared

Joel: cubed

Hypatia: plus 36

Barbara: square root

Horatio: divided by 5

Joel: times 50

Hypatia: minus 100

Barbara: times 6 billion

Horatio: plus 99

Joel: divided by 11

Hypatia: plus 1

Barbara: to the power of two

Horatio: minus 99

Joel: times itself 6 billion times

Hypatia: minus one

Barbara: divided by ten thousand

Horatio: plus 50

Joel: plus half of itself

Hypatia: plus 25

Barbara: minus 99

Horatio: cube root

Joel: next prime number above

Hypatia: ten’s complement

Barbara: second square number above

Horatio: reverse the digits

Joel: plus 3 more than six squared

Hypatia: minus 100

and so on!

As the kids get older, we gradually incorporate more sophisticated elements into the game, and take a little time out to explain to young Hypatia, for example, what it means to cube a number, to take a number to the power two, or what a prime number is. I remember playing the game with my math-savvy siblings when I was a kid, and the running number was sometimes something like $\sqrt 29$ or $2 + 3 𝑖$ , and a correspondingly full range of numbers and operations. It is fine to let the youngest drop out after a while, and continue with the older kids with more sophisticated operations; the youngsters will rejoin in the next round. In my childhood, we had a “challenge” rule, used when someone suspects that someone else doesn’t know the number: when challenged, the person should say the number; if incorrect, they are out, and otherwise the challenger is out.

Last weekend, I played the game with Horatio and Hypatia as we walked through Central Park to the Natural History Museum, and they conspired in whispering tones to mess me up, until finally I lost track of the number and they won…

Share:

Share:

Share:

Share:

Share:

Share:

Share:

Share:

Share:

Share:

Share:

Share:

Quarterfinals:

Semifinals:

Championship round:

Final Champion:

Share:

Share:

The number that must not be named

Share: