Tag Archives: elementary embeddings

Paul K. Gorbow, PhD 2018, University of Gothenburg

Posted on by
Reply

Paul K. Gorbow successfully defended his dissertation, “Self-similarity in the foundations” on June 14, 2018 at the University of Gothenburg in the Department of Philosophy, Linguistics and Theory of Science, under the supervision of Ali Enayat, with Peter LeFanu Lumsdaine and Zachiri McKenzie serving as secondary supervisors.  The defense opponent was Roman Kossak, with a dissertation committee consisting of Jon Henrik Forssell, Joel David Hamkins (myself) and Vera Koponen, chaired by Fredrik Engström. Congratulations!

University of Gothenburg profile |  ar$\chi$iv | Research Gate

Paul K. Gorbow, “Self-similarity in the foundations,” PhD dissertation for the University of Gothenburg, Acta Philosophica Gothoburgensia 32, June 2018. (arxiv:1806.11310)

Abstract. This thesis concerns embeddings and self-embeddings of foundational structures in both set theory and category theory. 

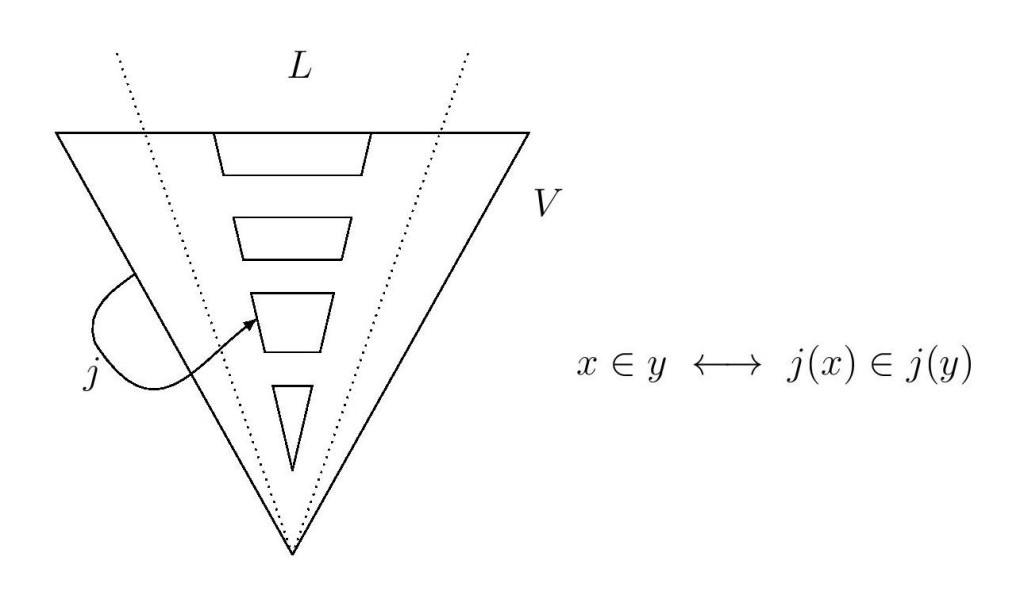
The first part of the work on models of set theory consists in establishing a refined version of Friedman’s theorem on the existence of embeddings between countable non-standard models of a fragment of ZF, and an analogue of a theorem of Gaifman to the effect that certain countable models of set theory can be elementarily end-extended to a model with many automorphisms whose sets of fixed points equal the original model. The second part of the work on set theory consists in combining these two results into a technical machinery, yielding several results about non-standard models of set theory relating such notions as self-embeddings, their sets of fixed points, strong rank-cuts, and set theories of different strengths.

The work in foundational category theory consists in the formulation of a novel algebraic set theory which is proved to be equiconsistent to New Foundations (NF), and which can be modulated to correspond to intuitionistic or classical NF, with or without atoms. A key axiom of this theory expresses that its structures have an endofunctor with natural properties.

In the Swedish style of dissertation defense, the opponent (in this case Roman Kossak) summarizes the dissertation, placing it in a broader context, and then challenges various parts of it, probing the candidate’s expertise in an extended discussion. What a pleasure it was to see this.  After this, there is a broader discussion, in which the committee is also involved.

The weakly compact embedding property, Apter-Gitik celebration, CMU 2015

Posted on by
2

This will be a talk at the Conference in honor of Arthur W. Apter and Moti Gitik at Carnegie Mellon University, May 30-31, 2015.  I am pleased to be a part of this conference in honor of the 60th birthdays of two mathematicians whom I admire very much.

Moti GitikArthur W. Apter

 

 

 

 

 

 

 

 

Abstract. The weakly compact embedding property for a cardinal $\kappa$ is the assertion that for every transitive set $M$ of size $\kappa$ with $\kappa\in M$, there is a transitive set $N$ and an elementary embedding $j:M\to N$ with critical point $\kappa$. When $\kappa$ is inaccessible, this property is one of many equivalent characterizations of $\kappa$ being weakly compact, along with the weakly compact extension property, the tree property, the weakly compact filter property and many others. When $\kappa$ is not inaccessible, however, these various properties are no longer equivalent to each other, and it is interesting to sort out the relations between them. In particular, I shall consider the embedding property and these other properties in the case when $\kappa$ is not necessarily inaccessible, including interesting instances of the embedding property at cardinals below the continuum, with relations to cardinal characteristics of the continuum.

This is joint work with Brent Cody, Sean Cox, myself and Thomas Johnstone.

Slides | Article | Conference web site

Carnegie Mellon University, College of Fine Arts

Embeddings of the universe into the constructible universe, current state of knowledge, CUNY Set Theory Seminar, March 2015

Posted on by
4

This will be a talk for the CUNY Set Theory Seminar, March 6, 2015.

I shall describe the current state of knowledge concerning the question of whether there can be an embedding of the set-theoretic universe into the constructible universe.

V to L

Question.(Hamkins) Can there be an embedding $j:V\to L$ of the set-theoretic universe $V$ into the constructible universe $L$, when $V\neq L$?

The notion of embedding here is merely that $$x\in y\iff j(x)\in j(y),$$ and such a map need not be elementary nor even $\Delta_0$-elementary. It is not difficult to see that there can generally be no $\Delta_0$-elementary embedding $j:V\to L$, when $V\neq L$.

Nevertheless, the question arises very naturally in the context of my previous work on the embeddability phenomenon, Every countable model of set theory embeds into its own constructible universe, where the title theorem is the following.

Theorem.(Hamkins) Every countable model of set theory $\langle M,\in^M\rangle$, including every countable transitive model of set theory, has an embedding $j:\langle M,\in^M\rangle\to\langle L^M,\in^M\rangle$ into its own constructible universe.

The methods of proof also established that the countable models of set theory are linearly pre-ordered by embeddability: given any two models, one of them embeds into the other; or equivalently, one of them is isomorphic to a submodel of the other. Indeed, one model $\langle M,\in^M\rangle$ embeds into another $\langle N,\in^N\rangle$ just in case the ordinals of the first $\text{Ord}^M$ order-embed into the ordinals of the second $\text{Ord}^N$. (And this implies the theorem above.)

In the proof of that theorem, the embeddings $j:M\to L^M$ are defined completely externally to $M$, and so it was natural to wonder to what extent such an embedding might be accessible inside $M$. And I realized that I could not generally refute the possibility that such a $j$ might even be a class in $M$.

Currently, the question remains open, but we have some partial progress, and have settled it in a number of cases, including the following, on which I’ll speak:

  • If there is an embedding $j:V\to L$, then for a proper class club of cardinals $\lambda$, we have $(2^\lambda)^V=(\lambda^+)^L$.
  • If $0^\sharp$ exists, then there is no embedding $j:V\to L$.
  • If $0^\sharp$ exists, then there is no embedding $j:V\to L$ and indeed no embedding $j:P(\omega)\to L$.
  • If there is an embedding $j:V\to L$, then the GCH holds above $\aleph_0$.
  • In the forcing extension $V[G]$ obtained by adding $\omega_1$ many Cohen reals (or more), there is no embedding $j:V[G]\to L$, and indeed, no $j:P(\omega)^{V[G]}\to V$. More generally, after adding $\kappa^+$ many Cohen subsets to $\kappa$, for any regular cardinal $\kappa$, then in $V[G]$ there is no $j:P(\kappa)\to V$.
  • If $V$ is a nontrivial set-forcing extension of an inner model $M$, then there is no embedding $j:V\to M$. Indeed, there is no embedding $j:P(\kappa^+)\to M$, if the forcing has size $\kappa$. In particular, if $V$ is a nontrivial forcing extension, then there is no embedding $j:V\to L$.
  • Every countable set $A$ has an embedding $j:A\to L$.

This is joint work of myself, W. Hugh Woodin, Menachem Magidor, with contributions also by David Aspero, Ralf Schindler and Yair Hayut.

See my related MathOverflow question: Can there be an embedding $j:V\to L$ from the set-theoretic universe $V$ to the constructible universe $L$, when $V\neq L$?

Talk Abstract