Tag Archives: absoluteness

Worldly cardinals are not always downwards absolute

Posted on by
3

 

UniversumI recently came to realize that worldly cardinals are not necessarily downward absolute to transitive inner models. That is, it can happen that a cardinal $\kappa$ is worldly in the full set-theoretic universe $V$, but not in some transitive inner model $W$, even when $W$ is itself a model of ZFC. The observation came out of some conversations I had with Alexander Block from Hamburg during his recent research visit to New York. Let me explain the argument.

A cardinal $\kappa$ is inaccessible, if it is an uncountable regular strong limit cardinal. The structure $V_\kappa$, consisting of the rank-initial segment of the set-theoretic universe up to $\kappa$, which can be generated from the empty set by applying the power set operation $\kappa$ many times, has many nice features. In particular, it is transitive model of $\newcommand\ZFC{\text{ZFC}}\ZFC$. The models $V_\kappa$ for $\kappa$ inaccessible are precisely the uncountable Grothendieck universes used in category theory.

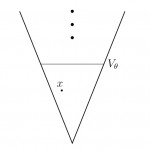
Although the inaccessible cardinals are often viewed as the entryway to the large cardinal hierarchy, there is a useful large cardinal concept weaker than inaccessibility. Namely, a cardinal $\kappa$ is worldly, if $V_\kappa$ is a model of $\ZFC$. Every inaccessible cardinal is worldly, and in fact a limit of worldly cardinals, because if $\kappa$ is inaccessible, then there is an elementary chain of cardinals $\lambda<\kappa$ with $V_\lambda\prec V_\kappa$, and all such $\lambda$ are worldly. The regular worldly cardinals are precisely the inaccessible cardinals, but the least worldly cardinal is always singular of cofinality $\omega$.

The worldly cardinals can be seen as a kind of poor-man’s inaccessible cardinal, in that worldliness often suffices in place of inaccessibility in many arguments, and this sometimes allows one to weaken a large cardinal hypothesis. But meanwhile, they do have some significant strengths. For example, if $\kappa$ is worldly, then $V_\kappa$ satisfies the principle that every set is an element of a transitive model of $\ZFC$.

It is easy to see that inaccessibility is downward absolute, in the sense that if $\kappa$ is inaccessible in the full set-theoretic universe $V$ and $W\newcommand\of{\subseteq}\of V$ is a transitive inner model of $\ZFC$, then $\kappa$ is also inaccessible in $W$. The reason is that $\kappa$ cannot be singular in $W$, since any short cofinal sequence in $W$ would still exist in $V$; and it cannot fail to be a strong limit there, since if some $\delta<\kappa$ had $\kappa$-many distinct subsets in $W$, then this injection would still exist in $V$. So inaccessibility is downward absolute.

The various degrees of hyper-inaccessibility are also downwards absolute to inner models, so that if $\kappa$ is an inaccessible limit of inaccessible limits of inaccessible cardinals, for example, then this is also true in any inner model. This downward absoluteness extends all the way through the hyperinaccessibility hierarchy and up to the Mahlo cardinals and beyond. A cardinal $\kappa$ is Mahlo, if it is a strong limit and the regular cardinals below $\kappa$ form a stationary set. We have observed that being regular is downward absolute, and it is easy to see that every stationary set $S$ is stationary in every inner model, since otherwise there would be a club set $C$ disjoint from $S$ in the inner model, and this club would still be a club in $V$. Similarly, the various levels of hyper-Mahloness are also downward absolute.

So these smallish large cardinals are generally downward absolute. How about the worldly cardinals? Well, we can prove first off that worldliness is downward absolute to the constructible universe $L$.

Observation. If $\kappa$ is worldly, then it is worldly in $L$.

Proof. If $\kappa$ is worldly, then $V_\kappa\models\ZFC$. This implies that $\kappa$ is a beth-fixed point. The $L$ of $V_\kappa$, which is a model of $\ZFC$, is precisely $L_\kappa$, which is also the $V_\kappa$ of $L$, since $\kappa$ must also be a beth-fixed point in $L$. So $\kappa$ is worldly in $L$. QED

But meanwhile, in the general case, worldliness is not downward absolute.

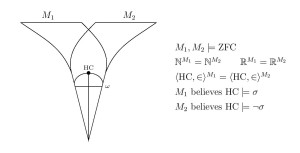
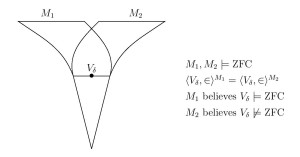
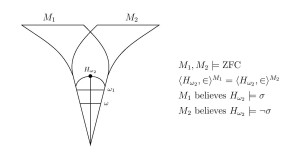
Theorem. Worldliness is not necessarily downward absolute to all inner models. It is relatively consistent with $\ZFC$ that there is a worldly cardinal $\kappa$ and an inner model $W\of V$, such that $\kappa$ is not worldly in $W$.

Proof. Suppose that $\kappa$ is a singular worldly cardinal in $V$. And by forcing if necessary, let us assume the GCH holds in $V$. Let $V[G]$ be the forcing extension where we perform the Easton product forcing $\newcommand\P{\mathbb{P}}\P$, so as to force a violation of the GCH at every regular cardinal $\gamma$. So the stage $\gamma$ forcing is $\newcommand\Q{\mathbb{Q}}\Q_\gamma=\text{Add}(\gamma,\gamma^{++})$.

First, I shall prove that $\kappa$ is worldly in the forcing extension $V[G]$. Since every set of rank less than $\kappa$ is added by some stage less than $\kappa$, it follows that $V_\kappa^{V[G]}$ is precisely $\bigcup_{\gamma<\kappa} V_\kappa[G_\gamma]$. Most of the $\ZFC$ axioms hold easily in $V_\kappa^{V[G]}$; the only difficult case is the collection axiom. And for this, by considering the ranks of witnesses, it suffices to show for every $\gamma<\kappa$ that every function $f:\gamma\to\kappa$ that is definable from parameters in $V_\kappa^{V[G]}$ is bounded. Suppose we have such a function, defined by $f(\alpha)=\beta$ just in case $\varphi(\alpha,\beta,p)$ holds in $V_\kappa^{V[G]}$. Let $\delta<\kappa$ be larger than the rank of $p$. Now consider $V_\kappa[G_\delta]$, which is a set-forcing extension of $V_\kappa$ and therefore a model of $\ZFC$. The fail forcing, from stage $\delta$ up to $\kappa$, is homogeneous in this model. And therefore we know that $f(\alpha)=\beta$ just in case $1$ forces $\varphi(\check\alpha,\check\beta,\check p)$, since these arguments are all in the ground model $V_\kappa[G_\delta]$. So the function is already definable in $V_\kappa[G_\delta]$. Because this is a model of $\ZFC$, the function $f$ is bounded below $\kappa$. So we get the collection axiom in $V_\kappa^{V[G]}$ and hence all of $\ZFC$ there, and so $\kappa$ is worldly in $V[G]$.

For any $A\of\kappa$, let $\P_A$ be the restriction of the Easton product forcing to include only the stages in $A$, and let $G_A$ be the corresponding generic filter. The full forcing $\P$ factors as $\P_A\times\P_{\kappa\setminus A}$, and so $V[G_A]\of V[G]$ is a transitive inner model of $\ZFC$.

But if we pick $A\of\kappa$ to be a short cofinal set in $\kappa$, which is possible because $\kappa$ is singular, then $\kappa$ will not be worldly in the inner model $V[G_A]$, since in $V_\kappa[G_A]$ we will be able to identify that sequence as the places where the GCH fails. So $\kappa$ is not worldly in $V[G_A]$.

In summary, $\kappa$ was worldly in $V[G]$, but not in the transitive inner model $W=V[G_A]$, and so worldliness is not downward absolute. QED

Same structure, different truths, Stanford University CSLI, May 2016

Posted on by
1

This will be a talk for the Workshop on Logic, Rationality, and Intelligent Interaction at the CSLI, Stanford University, May 27-28, 2016.

Abstract. To what extent does a structure determine its theory of truth? I shall discuss several surprising mathematical results illustrating senses in which it does not, for the satisfaction relation of first-order logic is less absolute than one might have expected. Two models of set theory, for example, can have exactly the same natural numbers and the same arithmetic structure $\langle\mathbb{N},+,\cdot,0,1,<\rangle$, yet disagree on what is true in this structure; they have the same arithmetic, but different theories of arithmetic truth; two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree on whether it is a well-order; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have a rank initial segment of the universe $\langle V_\delta,{\in}\rangle$ in common, yet disagree about whether it is a model of ZFC. These theorems and others can be proved with elementary classical model-theoretic methods, which I shall explain. 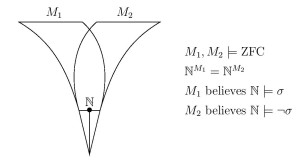Indefinite arithmetic truthOn the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I argue that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment.

Slides | Main article: Satisfaction is not absolute | CLSI 2016 | Abstract at CLSI

The absolute truth about non-absolute truth, JAF – Weak Arithmetics Days, New York, July 2015

Posted on by
Reply

This will be a talk for the Journées sur les Arithmétiques Faibles – Weak Arithmetics Days conference, held in New York at the CUNY Graduate Center, July 7 – 9, 2015.

Abstract. I will discuss several fun theorems and folklore results illustrating that the satisfaction relation of first-order logic is less absolute than one might have expected. Two models of set theory, for example, can have the same natural numbers $\langle\mathbb{N},+,\cdot,0,1,<\rangle$, yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree on whether it is a well-order and hence disagree about $\omega_1^{CK}$; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have a rank initial segment of the universe $\langle V_\delta,{\in}\rangle$ in common, yet disagree about whether it is a model of ZFC. These theorems and others can be proved with elementary classical model-theoretic methods. Indefinite arithmetic truthOn the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I have argued that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment.

Slides |  Main article: Satisfaction is not absolute

Does definiteness-of-truth follow from definiteness-of-objects? NY Philosophical Logic Group, NYU, November 2014

Posted on by
Reply

This will be a talk for the New York Philosophical Logic Group, November 10, 2014, 5-7pm, at the NYU Philosophy Department, 5 Washington Place, Room 302.

Indefinite arithmetic truth

Abstract. This talk — a mix of mathematics and philosophy — concerns the extent to which we may infer definiteness of truth in a mathematical context from definiteness of the underlying objects and structure of that context. The philosophical analysis is based in part on the mathematical observation that the satisfaction relation for model-theoretic truth is less absolute than often supposed.  Specifically, two models of set theory can have the same natural numbers and the same structure of arithmetic in common, yet disagree about whether a particular arithmetic sentence is true in that structure. In other words, two models can have the same arithmetic objects and the same formulas and sentences in the language of arithmetic, yet disagree on their corresponding theories of truth for those objects. Similarly, two models of set theory can have the same natural numbers, the same arithmetic structure, and the same arithmetic truth, yet disagree on their truths-about-truth, and so on at any desired level of the iterated truth-predicate hierarchy.  These mathematical observations, for which I shall strive to give a very gentle proof in the talk (using only elementary classical methods), suggest that a philosophical commitment to the determinate nature of the theory of truth for a structure cannot be seen as a consequence solely of the determinateness of the structure in which that truth resides. The determinate nature of arithmetic truth, for example, is not a consequence of the determinate nature of the arithmetic structure N = {0,1,2,…} itself, but rather seems to be an additional higher-order commitment requiring its own analysis and justification.

This work is based on my recent paper, Satisfaction is not absolute, joint with Ruizhi Yang (Fudan University, Shanghai).

Local properties in set theory

Posted on by
12

V_thetaSet-theoretic arguments often make use of the fact that a particular property $\varphi$ is local, in the sense that instances of the property can be verified by checking certain facts in only a bounded part of the set-theoretic universe, such as inside some rank-initial segment $V_\theta$ or inside the collection $H_\kappa$ of all sets of hereditary size less than $\kappa$. It turns out that this concept is exactly equivalent to the property being $\Sigma_2$ expressible in the language of set theory.

Theorem. For any assertion $\varphi$ in the language of set theory, the following are equivalent:

  1. $\varphi$ is ZFC-provably equivalent to a $\Sigma_2$ assertion.
  2. $\varphi$ is ZFC-provably equivalent to an assertion of the form “$\exists \theta\, V_\theta\models\psi$,” where $\psi$ is a statement of any complexity.
  3. $\varphi$ is ZFC-provably equivalent to an assertion of the form “$\exists \kappa\, H_\kappa\models\psi$,” where $\psi$ is a statement of any complexity.

Just to clarify, the $\Sigma_2$ assertions in set theory are those of the form $\exists x\,\forall y\,\varphi_0(x,y)$, where $\varphi_0$ has only bounded quantifiers. The set $V_\theta$ refers to the rank-initial segment of the set-theoretic universe, consisting of all sets of von Neumann rank less than $\theta$. The set $H_\kappa$ consists of all sets of hereditary size less than $\kappa$, that is, whose transitive closure has size less than $\kappa$.

Proof. ($3\to 2$) Since $H_\kappa$ is correctly computed inside $V_\theta$ for any $\theta>\kappa$, it follows that to assert that some $H_\kappa$ satisfies $\psi$ is the same as to assert that some $V_\theta$ thinks that there is some cardinal $\kappa$ such that $H_\kappa$ satisfies $\psi$.

($2\to 1$) The statement $\exists \theta\, V_\theta\models\psi$ is equivalent to the assertion $\exists\theta\,\exists x\,(x=V_\theta\wedge x\models\psi)$. The claim that $x\models\psi$ involves only bounded quantifiers, since the quantifiers of $\psi$ become bounded by $x$. The claim that $x=V_\theta$ is $\Pi_1$ in $x$ and $\theta$, since it is equivalent to saying that $x$ is transitive and the ordinals of $x$ are precisely $\theta$ and $x$ thinks every $V_\alpha$ exists, plus a certain minimal set theory (so far this is just $\Delta_0$, since all quantifiers are bounded), plus, finally, the assertion that $x$ contains every subset of each of its elements. So altogether, the assertion that some $V_\theta$ satisfies $\psi$ has complexity $\Sigma_2$ in the language of set theory.

($1\to 3$) This implication is a consequence of the following absoluteness lemma.

Lemma. (Levy) If $\kappa$ is any uncountable cardinal, then $H_\kappa\prec_{\Sigma_1} V$.

Proof. Suppose that $x\in H_\kappa$ and $V\models\exists y\,\psi(x,y)$, where $\psi$ has only bounded quantifiers. Fix some such witness $y$, which exists inside some $H_\gamma$ for perhaps much larger $\gamma$. By the Löwenheim-Skolem theorem, there is $X\prec H_\gamma$ with $\text{TC}(\{x\})\subset X$, $y\in X$ and $X$ of size less than $\kappa$. Let $\pi:X\cong M$ be the Mostowski collapse of $X$, so that $M$ is transitive, and since it has size less than $\kappa$, it follows that $M\subset H_\kappa$. Since the transitive closure of $\{x\}$ was contained in $X$, it follows that $\pi(x)=x$. Thus, since $X\models\psi(x,y)$ we conclude that $M\models \psi(x,\pi(y))$ and so hence $\pi(y)$ is a witness to $\psi(x,\cdot)$ inside $H_\kappa$, as desired. QED

Using the lemma, we now prove the remaining part of the theorem. Consider any $\Sigma_2$ assertion $\exists x\,\forall y\, \varphi_0(x,y)$, where $\varphi_0$ has only bounded quantifiers. This assertion is equivalent to $\exists\kappa\, H_\kappa\models\exists x\,\forall y\,\varphi_0(x,y)$, simply because if there is such a $\kappa$ with $H_\kappa$ having such an $x$, then by the lemma this $x$ works for all $y\in V$ since $H_\kappa\prec_{\Sigma_1}V$; and conversely, if there is an $x$ such that $\forall y\, \varphi_0(x,y)$, then this will remain true inside any $H_\kappa$ with $x\in H_\kappa$. QED

In light of the theorem, it makes sense to refer to the $\Sigma_2$ properties as the locally verifiable properties, or perhaps as semi-local properties, since positive instances of $\Sigma_2$ assertions can be verified in some sufficiently large $V_\theta$, without need for unbounded search. A truly local property, therefore, would be one such that positive and negative instances can be verified this way, and these would be precisely the $\Delta_2$ properties, whose positive and negative instances are locally verifiable.

Tighter concepts of locality are obtained by insisting that the property is not merely verified in some $V_\theta$, perhaps very large, but rather is verified in a $V_\theta$ where $\theta$ has a certain closeness to the parameters or instance of the property. For example, a cardinal $\kappa$ is measurable just in case there is a $\kappa$-complete nonprincipal ultrafilter on $\kappa$, and this is verified inside $V_{\kappa+2}$. Thus, the assertion “$\kappa$ is measurable,” has complexity $\Sigma^2_1$ over $V_\kappa$. One may similarly speak of $\Sigma^n_m$ or $\Sigma^\alpha_m$ properties, to refer to properties that can be verified with $\Sigma_m$ assertions in $V_{\kappa+\alpha}$. Alternatively, for any class function $f$ on the ordinals, one may speak of $f$-local properties, meaning a property that can be checked of $x\in V_\theta$ by checking a property inside $V_{f(\theta)}$.

This post was made in response to a question on MathOverflow.

Satisfaction is not absolute, Dartmouth Logic Seminar, January 2014

Posted on by
Reply

dartmouth_campusThis will be a talk for the Dartmouth Logic Seminar on January 23rd, 2014.

Abstract. I will discuss a number of theorems showing that the satisfaction relation of first-order logic is less absolute than might have been supposed. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic $\langle\mathbb{N},{+},{\cdot},0,1,{\lt}\rangle$, yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree on whether it is a well-order; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have a rank initial segment of the universe $\langle V_\delta,{\in}\rangle$ in common, yet disagree about whether it is a model of ZFC. The theorems are proved with elementary classical model-theoretic methods, and many of them can be considered folklore results in the subject of models of arithmetic.

Indefinite arithmetic truthOn the basis of these mathematical results, Ruizhi Yang (Fudan University, Shanghai) and I have argued that the definiteness of truth in a structure, such as with arithmetic truth in the standard model of arithmetic, cannot arise solely from the definiteness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.

Main article: Satisfaction is not absolute

Satisfaction is not absolute

Posted on by
22

[bibtex key=HamkinsYang:SatisfactionIsNotAbsolute]$\newcommand\N{\mathbb{N}}\newcommand\satisfies{\models}$

Abstract. We prove that the satisfaction relation $\mathcal{N}\satisfies\varphi[\vec a]$ of first-order logic is not absolute between models of set theory having the structure $\mathcal{N}$ and the formulas $\varphi$ all in common. Two models of set theory can have the same natural numbers, for example, and the same standard model of arithmetic $\langle\N,{+},{\cdot},0,1,{\lt}\rangle$, yet disagree on their theories of arithmetic truth; two models of set theory can have the same natural numbers and the same arithmetic truths, yet disagree on their truths-about-truth, at any desired level of the iterated truth-predicate hierarchy; two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth; two models of set theory can have the same $\langle H_{\omega_2},{\in}\rangle$ or the same rank-initial segment $\langle V_\delta,{\in}\rangle$, yet disagree on which assertions are true in these structures.

On the basis of these mathematical results, we argue that a philosophical commitment to the determinateness of the theory of truth for a structure cannot be seen as a consequence solely of the determinateness of the structure in which that truth resides. The determinate nature of arithmetic truth, for example, is not a consequence of the determinate nature of the arithmetic structure $\N=\{ 0,1,2,\ldots\}$ itself, but rather, we argue, is an additional higher-order commitment requiring its own analysis and justification.

Many mathematicians and philosophers regard the natural numbers $0,1,2,\ldots\,$, along with their usual arithmetic structure, as having a privileged mathematical existence, a Platonic realm in which assertions have definite, absolute truth values, independently of our ability to prove or discover them. Although there are some arithmetic assertions that we can neither prove nor refute—such as the consistency of the background theory in which we undertake our proofs—the view is that nevertheless there is a fact of the matter about whether any such arithmetic statement is true or false in the intended interpretation. The definite nature of arithmetic truth is often seen as a consequence of the definiteness of the structure of arithmetic $\langle\N,{+},{\cdot},0,1,{\lt}\rangle$ itself, for if the natural numbers exist in a clear and distinct totality in a way that is unambiguous and absolute, then (on this view) the first-order theory of truth residing in that structure—arithmetic truth—is similarly clear and distinct.

Feferman provides an instance of this perspective when he writes (Feferman 2013, Comments for EFI Workshop, p. 6-7) :

In my view, the conception [of the bare structure of the natural numbers] is completely clear, and thence all arithmetical statements are definite.

It is Feferman’s `thence’ to which we call attention.  Martin makes a similar point (Martin, 2012, Completeness or incompleteness of basic mathematical concepts):

What I am suggesting is that the real reason for confidence in first-order completeness is our confidence in the full determinateness of the concept of the natural numbers.

Many mathematicians and philosophers seem to share this perspective. The truth of an arithmetic statement, to be sure, does seem to depend entirely on the structure $\langle\N,{+},{\cdot},0,1,{\lt}\rangle$, with all quantifiers restricted to $\N$ and using only those arithmetic operations and relations, and so if that structure has a definite nature, then it would seem that the truth of the statement should be similarly definite.

Nevertheless, in this article we should like to tease apart these two ontological commitments, arguing that the definiteness of truth for a given mathematical structure, such as the natural numbers, the reals or higher-order structures such as $H_{\omega_2}$ or $V_\delta$, does not follow from the definite nature of the underlying structure in which that truth resides. Rather, we argue that the commitment to a theory of truth for a structure is a higher-order ontological commitment, going strictly beyond the commitment to a definite nature for the underlying structure itself.

We make our argument in part by proving that different models of set theory can have a structure identically in common, even the natural numbers, yet disagree on the theory of truth for that structure.

Theorem.

  • Two models of set theory can have the same structure of arithmetic $$\langle\N,{+},{\cdot},0,1,{\lt}\rangle^{M_1}=\langle\N,{+},{\cdot},0,1,{\lt}\rangle^{M_2},$$yet disagree on the theory of arithmetic truth.
  • Two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree about whether it is a well-order.
  • Two models of set theory that have the same natural numbers and the same reals, yet disagree on projective truth.
  • Two models of set theory can have a transitive rank initial segment in common $$\langle V_\delta,{\in}\rangle^{M_1}=\langle V_\delta,{\in}\rangle^{M_2},$$yet disagree about whether it is a model of ZFC.

The proofs use only elementary classical methods, and might be considered to be a part of the folklore of the subject of models of arithmetic. The paper includes many further examples of the phenomenon, and concludes with a philosophical discussion of the issue of definiteness, concerning the question of whether one may deduce definiteness-of-truth from definiteness-of-objects and definiteness-of-structure.

 

Satisfaction is not absolute, CUNY Logic Workshop, September 2013

Posted on by
2

This will be a talk for the CUNY Logic Workshop on September 27, 2013.

Abstract.  I will discuss a number of theorems showing that the satisfaction relation of first-order logic is less absolute than might have been supposed. Two models of set theory $M_1$ and $M_2$, for example, can agree on their natural numbers $\langle\mathbb{N},{+},{\cdot},0,1,{\lt}\rangle^{M_1}=\langle\mathbb{N},{+},{\cdot},0,1,{\lt}\rangle^{M_2}$, yet disagree on arithmetic truth: they have a sentence $\sigma$ in the language of arithmetic that $M_1$ thinks is true in the natural numbers, yet $M_2$ thinks $\neg\sigma$ there. Two models of set theory can agree on the natural numbers $\mathbb{N}$ and on the reals $\mathbb{R}$, yet disagree on projective truth. Two models of set theory can have the same natural numbers and have a computable linear order in common, yet disagree about whether this order is well-ordered. Two models of set theory can have a transitive rank initial segment $V_\delta$ in common, yet disagree about whether this $V_\delta$ is a model of ZFC. The theorems are proved with elementary classical methods.

This is joint work with Ruizhi Yang (Fudan University, Shanghai). We argue, on the basis of these mathematical results, that the definiteness of truth in a structure, such as with arithmetic truth in the standard model of arithmetic, cannot arise solely from the definiteness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.

Article

Satisfaction is not absolute, Connecticut, October 2013

Posted on by
4

This will be a talk for the Logic Seminar in the Mathematics Department at the University of Connecticut in Storrs on October 25, 2013.

Abstract. The satisfaction relation $\mathcal{N}\models\varphi[\vec a]$ of first-order logic, it turns out, is less absolute than might have been supposed.  Two models of set theory, for example, can agree on their natural numbers and on what they think is the standard model of arithmetic $\langle\mathbb{N},{+},{\cdot},0,1,{\lt}\rangle$, yet disagree on their theories of arithmetic truth, the first-order truths of this structure.  Two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth.  Two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree about whether it is well-ordered.  Two models of set theory can have a transitive rank initial segment $V_\delta$ in common, yet disagree about whether it is a model of ZFC.  The arguments rely mainly on elementary classical methods.

This is joint work with Ruizhi Yang (Fudan University, Shanghai), and our manuscript will be available soon, in which we prove these and several other very general facts showing that satisfaction is not absolute.  On the basis of these mathematical results, we mount a philosophical argument that a commitment to the determinateness of truth in a structure, such as the case of arithmetic truth in the standard model of arithmetic, cannot result solely from the determinateness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.

University of Connecticut Logic Seminar | Article