This was a talk at the upcoming International Workshop in Set Theory at the Centre International de Rencontres Mathématiques at the Luminy campus in Marseille, France, October 9-13, 2017.
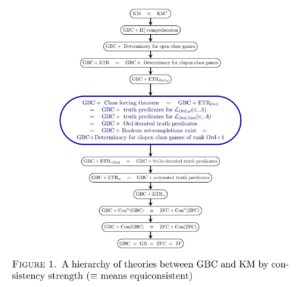
Abstract. Recent work has clarified how various natural second-order set-theoretic principles, such as those concerned with class forcing or with proper class games, fit into a new robust hierarchy of second-order set theories between Gödel-Bernays GBC set theory and Kelley-Morse KM set theory and beyond. For example, the principle of clopen determinacy for proper class games is exactly equivalent to the principle of elementary transfinite recursion ETR, strictly between GBC and GBC+$\Pi^1_1$-comprehension; open determinacy for class games, in contrast, is strictly stronger; meanwhile, the class forcing theorem, asserting that every class forcing notion admits corresponding forcing relations, is strictly weaker, and is exactly equivalent to the fragment $\text{ETR}_{\text{Ord}}$ and to numerous other natural principles. What is emerging is a higher set-theoretic analogue of the familiar reverse mathematics of second-order number theory.
https://plus.google.com/u/0/+JoelDavidHamkins1/posts/ekgdakenadv
It’s great to see that people are looking at this interesting issue. Two questions:
1. I know that strong choice principles for classes are largely independent of KM, is there work examining the consistency strength of these principles? More generally, is there much of a space above KM?
2. I wonder where the Welch embedding $j: M \longrightarrow V$ might fit in here (say added over GBC or KM). While necessarily second-order, that doesn’t clearly fit into the template you’ve got there, and substantially goes beyond any of the theories outlined in terms of consistency strength (in virtue of the large cardinals it implies). [Years ago I had an idea to try and reverse over the existence of such an embedding, but couldn’t get anything other than the very trivial.]
3. More speculatively: Clearly this slots nicely into your Multiverse View. However, do you think there are substantial differences in argumentation for Multiversism between the first-order and second-order claims? It’s interesting because there seems to be less of a `zoo’ of worlds, and you don’t obviously get incompatibility (perhaps because of inattention due to metamathematical quibbles)? Is there a philosophical equivalent of CH and ~CH in the second-order case?
Best,
Neil
Thanks for your comments, Neil, I’m glad you find the topic interesting. Let me respond to the points you raise.
1. KM is equiconsistent with KM+, which has the class-choice principle, and so there is no increase in consistency strength to add class-choice. Indeed, it is conservative over KM for first-order assertions, since every KM model has a KM+ realization with the same sets.
2. The embeddings j:M to V, however, have a consistency strength on the order of “Ord is Ramsey” according to the Vickers and Welch result, so this consistency strength does go beyond KM. I think that this axiom is expressible in second-order set theory, since M and j are classes, and so it would fit into the hierarchy, but the strength is beyond KM. (Note that KM itself is weaker in consistency strength than ZFC + there is an inaccessible cardinal, which is fairly mild by large cardinal standards.
3. That is interesting. It seems to me that there is a huge diversity of models of the second-order theory, since most of the variations in first-order set theory carry over to this realm. So we can consider models of GBC with CH or GCH or not or with large cardinals and so on. A difference, however, is to look at how one can make changes in the second-order part of a model, while keeping the same first-order part. My student Kameryn Williams has some results in this perspective.
Thanks for your responses Joel!
A quick follow up on (2.): For sure the consistency strength will be way higher, but I’m wondering if such a j directly *implies* other class principles. So, for example, if I add such a j over NBG, can I get any class comprehension? There’s at least some places where they converge (e.g. in both $\Pi^1_1$-Comp and $NBG + \exists j: M \to V$ you can get a first-order truth definition.
I’m looking forward to speaking to Kameryn (we’ve had a couple of e-mail interchanges already).