Category Archives: Talks

Address at the Dean's List Ceremony

Posted on by
4

As the designated faculty speaker, selected after nominations from all the various departments at the college, I made the following remarks, in full academic regalia, at the Dean’s List ceremony this evening at the College of Staten Island.

College of Staten IslandThank you very much to the Dean for the kind introduction.

I am pleased and honored to be here, amongst the elite of the College of Staten Island, students who have made the Dean’s list for academic accomplishment. You have proved yourselves in the challenges of academic life and you should be proud. I am proud of you.

You are our intellectual powers, engines of thought and reason. Probably your minds are running all the time—it does seem a little hot in here…

In the classic Wim Wenders film, “Wings of Desire,” some characters are able to hear and experience the thoughts of others. And although one ordinarily imagines a library as a place of quiet contemplation, in the film the library was a cacophy of voices, a hundred trains of thought running through, each audibly expressing the content of a person’s mind.

This is how I like to imagine the arena of the mind, lively and exciting.

But also playful. Perhaps I’m called on to offer some advice to you, and my advice is this: pursue an attitude of playful curiosity about your subject, whatever it is. Play with new ideas, explore all facets of them, going beyond whatever had been expected of you. You will be led to vast new lands of imagination. 

A while back, my son Horatio, in fourth grade at the time, showed me his math homework. His teacher had said, “I am thinking of a number. It has a 3 in the ten’s place. The digits add to 10. It is prime. What is my number?” Can anyone solve it? Yes, 37 is a solution, and Horatio also had found it. He asked me, “are there other solutions?”  Now perhaps an unimaginative person might think only of two-digit numbers, and in this case, 37 is the only solution. But with imagination, we can seek out larger possibilities. And indeed Horatio and I worked together at the cafe and realized that 433 is another solution, as well as 631 and 1531. I checked a table of prime numbers, and found that 10333 is also a solution, as is 100,333.  I began to wonder:  are there infinitely many solutions? I had no idea how to prove such a thing.

So I posted the question to one of the math Q & A sites, and it immediately rocketed to the top, getting thousands of views. Mathematicians all around the world were thinking about this playful version of my son’s homework problem. Some of these mathematicians wrote computer programs to find more and more
solutions; one young mathematician found all the solutions up to one hundred million, systematically. Another found enormous solutions, gigantic prime numbers, one with 416 digits (mostly zeros), which were also solutions of the problem. But with regard to whether there are infinitely many solutions or not, we still had no answer.  It turns out to be an open mathematical question;  nobody knows, and the question leads to deep number-theoretic waters. 

Another instance of playfulness began when I was a graduate student. A prominent visiting mathematician (Lenore Blum) gave a talk about the theory of infinitely precise computation, concerning computational devices able to undertake perfectly accurate real number arithmetic. After the talk, inspired, a group of us speculated about other infinitary notions of computability: what could or should one do with a computational device able to undertake infinitely many steps of computation? We played with the idea, and over several years a theory gradually emerged.  Although some of my research colleagues had discouraged me, I ignored them and continued to play with and develop my theory. In time, our ideas grew into a new theory of infinitary computation. We had invented the subject now known as infinite time Turing machines. Those playful ideas led to a new theory that is now studied around the world, with new masters theses written on it and Ph.D. dissertations written on it, and conferences focused on it; our original article now has hundreds of citations.

Play is not always easy. It took years of seriously hard work in the case I just mentioned; but essential to that work was play. So please play! Explore your ideas further, and see where they take you!

Thank you very much.

Satisfaction is not absolute, CUNY Logic Workshop, September 2013

Posted on by
2

This will be a talk for the CUNY Logic Workshop on September 27, 2013.

Abstract.  I will discuss a number of theorems showing that the satisfaction relation of first-order logic is less absolute than might have been supposed. Two models of set theory M1 and M2, for example, can agree on their natural numbers ⟨N,+,⋅,0,1,<⟩M1=⟨N,+,⋅,0,1,<⟩M2, yet disagree on arithmetic truth: they have a sentence σ in the language of arithmetic that M1 thinks is true in the natural numbers, yet M2 thinks ¬σ there. Two models of set theory can agree on the natural numbers N and on the reals R, yet disagree on projective truth. Two models of set theory can have the same natural numbers and have a computable linear order in common, yet disagree about whether this order is well-ordered. Two models of set theory can have a transitive rank initial segment Vδ in common, yet disagree about whether this Vδ is a model of ZFC. The theorems are proved with elementary classical methods.

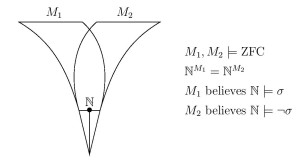This is joint work with Ruizhi Yang (Fudan University, Shanghai). We argue, on the basis of these mathematical results, that the definiteness of truth in a structure, such as with arithmetic truth in the standard model of arithmetic, cannot arise solely from the definiteness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.

Article

The role of the axiom of foundation in the Kunen inconsistency, CUNY September 2013

Posted on by
4

This will be a talk for the CUNY Set Theory Seminar on September 20, 2013 (date tentative).

Abstract. The axiom of foundation plays an interesting role in the Kunen inconsistency, the assertion that there is no nontrivial elementary embedding of the set-theoretic universe to itself, for the truth or falsity of the Kunen assertion depends on one’s specific anti-foundational stance.  The fact of the matter is that different anti-foundational theories come to different conclusions about this assertion.  On the one hand, it is relatively consistent with ZFC without foundation that the Kunen assertion fails, for there are models of  ZFC-F  in which there are definable nontrivial elementary embeddings j:V→V. Indeed, in Boffa’s anti-foundational theory BAFA, the Kunen assertion is outright refutable, and in this theory there are numerous nontrivial elementary embeddings of the universe to itself. Meanwhile, on the other hand, Aczel’s anti-foundational theory GBC-F+AFA, as well as Scott’s theory GBC-F+SAFA and other anti-foundational theories, continue to prove the Kunen assertion, ruling out the existence of a nontrivial elementary embedding j:V→V.

This talk covers very recent joint work with Emil Jeřábek, Ali Sadegh Daghighi and Mohammad Golshani, based on an interaction growing out of Ali’s question on MathOverflow, which lead to our recent article, The role of the axiom of foundation in the Kunen inconsistency.

Exploring the Frontiers of Incompleteness, Harvard, August 2013

Posted on by
Reply

I will be participating in the culminating workshop of the Exploring the Frontiers of Incompleteness conference series at Harvard University, to take place August 31-September 1, 2013.  Rather than conference talks, the program will consist of extended discussion sessions by the participants of the year-long series, with the discussion framed by very brief summary presentations.  Peter Koellner asked me to prepare such a presentation on the multiverse conception, and you can see the slides in The multiverse perspective in set theory (Slides).

My previous EFI talk was The multiverse perspective on determinateness in set theory, based in part on my paper The set-theoretical multiverse.

Satisfaction is not absolute, Connecticut, October 2013

Posted on by
4

This will be a talk for the Logic Seminar in the Mathematics Department at the University of Connecticut in Storrs on October 25, 2013.

Abstract. The satisfaction relation N⊨φ[a→] of first-order logic, it turns out, is less absolute than might have been supposed.  Two models of set theory, for example, can agree on their natural numbers and on what they think is the standard model of arithmetic ⟨N,+,⋅,0,1,<⟩, yet disagree on their theories of arithmetic truth, the first-order truths of this structure.  Two models of set theory can have the same natural numbers and the same reals, yet disagree on projective truth.  Two models of set theory can have the same natural numbers and a computable linear order in common, yet disagree about whether it is well-ordered.  Two models of set theory can have a transitive rank initial segment Vδ in common, yet disagree about whether it is a model of ZFC.  The arguments rely mainly on elementary classical methods.

This is joint work with Ruizhi Yang (Fudan University, Shanghai), and our manuscript will be available soon, in which we prove these and several other very general facts showing that satisfaction is not absolute.  On the basis of these mathematical results, we mount a philosophical argument that a commitment to the determinateness of truth in a structure, such as the case of arithmetic truth in the standard model of arithmetic, cannot result solely from the determinateness of the structure itself in which that truth resides; rather, it must be seen as a separate, higher-order ontological commitment.

University of Connecticut Logic Seminar | Article

Workshop on paraconsistent set theory, Connecticut, October 2013

Posted on by
17

I’ll be participating in a workshop at the University of Connecticut, Storrs, philosophy department on October 26-27, 2013, on paraconsistent set theory, organized by Graham Priest and JC Beall.  I am given to understand that part of the goal is to develop additional or improved model-construction methods, with which one might expand the range of possible behaviors that we know about.

Universal structures: the countable random graph, the surreal numbers and the hypnagogic digraph, Swarthmore College, October 2013

Posted on by
2

I’ll be speaking for the Swarthmore College Mathematics and Statistics Colloquium on October 8th, 2013.

220px-Swarthmore_College_Logo_Current

 

 

 

 

Abstract.  I’ll be giving an introduction to universal structures in mathematics, where a structure M is universal for a class of structures, if every structure in that class arises as (isomorphic to) a substructure of M.  For example, Cantor proved that the rational line Q is universal for all countable linear orders.  Is a corresponding fact true of the real line for linear orders of that size? Are there countably universal partial orders? Is there a countably universal graph? directed graph? acyclic digraph?  Is there a countably universal group? We’ll answer all these questions and more, with an account of the countable random graph, generalizations to the random graded digraphs, Fraïssé limits, the role of saturation, the surreal numbers and the hypnagogic digraph.  The talk will conclude with some very recent work on universality amongst the models of set theory.

Poster

Embeddability amongst the countable models of set theory, plenary talk for ASL / Joint Math Meetings in Baltimore, January 2014

Posted on by
5

A one-hour plenary talk for the ASL at the Joint Math Meetings, January 15-18, 2014 in Baltimore, MD.

Saturday January 18, 2014, 2:00 p.m.-2:50 p.m, Room 319 BCC

Abstract. A surprisingly vigorous embeddability phenomenon has recently been uncovered amongst the countable models of set theory.  In particular, embeddability is linear:  for any two countable models of set theory, one of them is isomorphic to a submodel of the other.  In particular, every countable model of set theory, including every well-founded model, is isomorphic to a submodel of its own constructible universe, so that there is an embedding j:M→LM for which x∈y⟺j(x)∈j(y). The proof uses universal digraph combinatorics, including an acyclic version of the countable random digraph, which I call the countable random Q-graded digraph, and higher analogues arising as uncountable Fraïssé limits, leading to the hypnagogic digraph, a set-homogeneous, class-universal, surreal-numbers-graded acyclic class digraph, closely connected with the surreal numbers.

Slides | Article | JMM Schedule

Panelist at the Infinity Salon for the World Science Festival, NYC, June 2013

Posted on by
3

The World Science Festival is coming to New York (May 29 — June 2), with numerous interesting events, including the infinity salon, an intimate, free-wheeling discussion about infinity, entitled The future of Infinity:  Solving Math’s most notorious problem, for an audience of experts.

I shall be on the panel along with Steven Strogatz, W. Hugh Woodin and others,  moderated by Keith Devlin.

I’m looking forward to it!

(Note that tickets are required for many events.)

From the salon web site:

Saturday, June 1, 2013

3:30 PM – 5:00 PM

 

In 1873, Georg Cantor proved that there are different sizes of infinity. Cantor tried to answer the question by proposing the Continuum Hypothesis. A solution of sorts was found in 1963, but the answer—proof that there was no proof—raised questions about the foundations of mathematics. Most deemed that counting the infinite was beyond mathematical precision. Recently, progress has been made, and the Continuum Hypothesis might have a definite answer—true or false.

 

The World Science Festival’s annual salon series offers in-depth conversations with leading scientists, extending the discussion of the Festival’s premiere public programs to graduate students, postdocs, faculty and well-informed members of the general public.

Keith Devlin’s blog post about the discussion

Universality, saturation and the surreal number line, Shanghai, June 2013

Posted on by
Reply

Fudan bridgeThis will be a short lecture series given at the conclusion of the graduate logic class in the Mathematical Logic group at Fudan University in Shanghai, June 13, 18 (or 20), 2013.

I will present an elementary introduction to the theory of universal orders and relations and saturated structures.  We’ll start with the classical fact, proved by Cantor, that the rational line is the universal countable linear order.  But what about universal partial orders, universal graphs and other mathematical structures?  Is there a computable universal partial order?  What is the countable random graph? Which orders embed into  the power set of the natural numbers under the subset relation ⟨P(N),⊂⟩? Proceeding to larger and larger universal orders, we’ll eventually arrive at the surreal numbers and the hypnagogic digraph.

Fudan University seal

 

Playing go with Jiachen

Playful paradox with large numbers, infinity and logic, Shanghai, June 2013

Posted on by
1

Playful paradox

This will be a talk at Fudan University in Shanghai, China, June 12, 2013, sponsored by the group in Mathematical Logic at Fudan, for a large audience of students.

Abstract: For success in mathematics and science, I recommend an attitude of playful curiosity about one’s subject. We shall accordingly explore a number of puzzling conundrums at the foundations of mathematics concerning issues with large numbers, infinity and logic. These are serious issues—and we’ll have serious things to say—while still having fun. Can one complete a task involving infinitely many steps? Are there some real numbers that in principle cannot be described? Is every true statement provable? Does every mathematical problem ultimately reduce to computational procedure? What is the largest natural number that can be written or described in ordinary type Fudan University seal on an index card? Which is bigger, a googol-bang-plex or a googol-plex-bang? Is every natural number interesting? Is every sentence either true or false or neither true nor false? We will explore these and many other puzzles and paradoxes involving large numbers, logic and infinity, and along the way, learn some interesting mathematics and philosophy.   The Largest-Number Contest.  In preparation for the talk, and with a nod to Douglas Hofstadter, we shall be holding a contest:  Who can describe the largest number on an ordinary index card?   See the contest announcement poster.

  1. A submission entry consists of the description of a positive integer written on an ordinary index card, using common mathematical operations and notation or English words and phrases.
  2. Write legibly, and use at most 100 symbols from the ordinary ASCII character set.  Bring your submission to the talk.
  3. Descriptions that fail to describe a number are disqualified.
  4. The submission with the largest number wins.
  5. The prize will be $1 million USD divided by the winning number itself, rounded to the nearest cent, plus another small token prize.

Example submissions: 

99999.

10*(10*99)+5

The population of Shanghai at this moment.

Read a more detailed account of the contest and its results.

Algebraicity and implicit definability in set theory, CUNY, May 2013

Posted on by
3

This is a talk May 10, 2013 for the CUNY Set Theory Seminar.

Abstract.  An element a is definable in a model M if it is the unique object in M satisfying some first-order property. It is algebraic, in contrast, if it is amongst at most finitely many objects satisfying some first-order property φ, that is, if { b | M satisfies φ[b] } is a finite set containing a. In this talk, I aim to consider the situation that arises when one replaces the use of definability in several parts of set theory with the weaker concept of algebraicity. For example, in place of the class HOD of all hereditarily ordinal-definable sets, I should like to consider the class HOA of all hereditarily ordinal algebraic sets. How do these two classes relate? In place of the study of pointwise definable models of set theory, I should like to consider the pointwise algebraic models of set theory. Are these the same? In place of the constructible universe L, I should like to consider the inner model arising from iterating the algebraic (or implicit) power set operation rather than the definable power set operation. The result is a highly interesting new inner model of ZFC, denoted Imp, whose properties are only now coming to light. Is Imp the same as L? Is it absolute? I shall answer all these questions at the talk, but many others remain open.

This is joint work with Cole Leahy (MIT).

NYlogic abstract | MathOverflow post

The theory of infinite games, with examples, including infinite chess

Posted on by
2

This will be a talk on April 30, 2013 for a joint meeting of the Yeshiva University Mathematics Club and the  Yeshiva University Philosophy Club.  The event will take place in 5:45 pm in Furst Hall, on the corner of Amsterdam Ave. and 185th St.

Abstract. I will give a general introduction to the theory of infinite games, suitable for mathematicians and philosophers.  What does it mean to play an infinitely long game? What does it mean to have a winning strategy for such a game?  Is there any reason to think that every game should have a winning strategy for one player or another?  Could there be a game, such that neither player has a way to force a win?  Must every computable game have a computable winning strategy?  I will present several game paradoxes and example infinitary games, including an infinitary version of the game of Nim, and several examples from infinite chess.

NYlogic entry | Yeshiva University | Infinite chess | Video

 

Pluralism in mathematics: the multiverse view in set theory and the question of whether every mathematical statement has a definite truth value, Rutgers, March 2013

Posted on by
Reply

This is a talk for the Rutgers Logic Seminar on March 25th, 2013.  Simon Thomas specifically requested that I give a talk aimed at philosophers.

Abstract.  I shall describe the debate on pluralism in the philosophy of set theory, specifically on the question of whether every mathematical and set-theoretic assertion has a definite truth value. A traditional Platonist view in set theory, which I call the universe view, holds that there is an absolute background concept of set and a corresponding absolute background set-theoretic universe in which every set-theoretic assertion has a final, definitive truth value. I shall try to tease apart two often-blurred aspects of this perspective, namely, to separate the claim that the set-theoretic universe has a real mathematical existence from the claim that it is unique. A competing view, the multiverse view, accepts the former claim and rejects the latter, by holding that there are many distinct concepts of set, each instantiated in a corresponding set-theoretic universe, and a corresponding pluralism of set-theoretic truths. After framing the dispute, I shall argue that the multiverse position explains our experience with the enormous diversity of set-theoretic possibility, a phenomenon that is one of the central set-theoretic discoveries of the past fifty years and one which challenges the universe view. In particular, I shall argue that the continuum hypothesis is settled on the multiverse view by our extensive knowledge about how it behaves in the multiverse, and as a result it can no longer be settled in the manner formerly hoped for.

Some of this material arises in my recent articles: