Tag Archives: KM

Every worldly cardinal admits a Gödel-Bernays structure

Posted on by
2

My Oxford student Emma Palmer and I have been thinking about worldly cardinals and Gödel-Bernays GBC set theory, and we recently came to a new realization.

Namely, what I realized is that every worldly cardinal $\kappa$ admits a Gödel-Bernays structure, including the axiom of global choice. That is, if $\kappa$ is worldly, then there is a family $X$ of sets so that $\langle V_\kappa,\in,X\rangle$ is a model of Gödel-Bernays set theory GBC including global choice.

For background, it may be helpful to recall Zermelo’s famous 1930 quasi-categoricity result, showing that the inaccessible cardinals are precisely the cardinals $\kappa$ for which $V_\kappa$ is a model of second-order set theory $\text{ZFC}_2$.

If one seeks only the first-order ZFC set theory in $V_\kappa$, however, then this is what it means to say that $\kappa$ is a worldly cardinal, a strictly weaker notion. That is, $\kappa$ is worldly if and only if $V_\kappa\models\text{ZFC}$. Every inaccessible cardinal is worldly, by Zermelo’s result. But more, every inaccessible is a limit of worldly cardinals, and so there are many worldly cardinals that are not inaccessible. The least worldly cardinal, for example, has cofinality $\omega$. Indeed, the next worldly cardinal above any ordinal has cofinality $\omega$.

Meanwhile, to improve slightly on Zermelo, we can observe that if $\kappa$ is inaccessible, then $V_\kappa$ is a model of Kelley-Morse set theory when equipped with the full second-order complement of classes. That is, $\langle V_\kappa,\in,V_{\kappa+1}\rangle$ is a model of KM.

This is definitely not true when $\kappa$ is merely worldly and not inaccessible, however, for in this case $\langle V_\kappa,\in,V_{\kappa+1}\rangle$ is never a model of KM nor even GBC when $\kappa$ is singular. The reason is that the singularity of $\kappa$ would be revealed by a short cofinal sequence, which would be available in the full power set $V_{\kappa)+1}=P(V_\kappa)$, and this would violate replacement.

So the question is:

Question. If $\kappa$ is worldly, then can we equip $V_\kappa$ with a suitable family $X$ of classes so that $\langle V_\kappa,\in,X\rangle$ is a model of GBC?

The answer is Yes!

What I claim is that for every worldly cardinal $\kappa$, there is a definably generic well order $\newcommand\slantleq{\mathrel{⩽}}\slantleq$ of $V_\kappa$, so that the subsets definable in $\langle V_\kappa,\in,\slantleq\rangle$ make a model of GBC.

To see this, consider the class forcing notion $\newcommand\P{\mathbb{P}}\P$ for adding a global well order $\slantleq$, as $V_\kappa$ sees it. Conditions are well orders of some $V_\alpha$ for some $\alpha<\kappa$, ordered by end-extension, so that lower rank sets always preceed higher rank sets in the resulting order.

I shall prove that there is a well-order $\slantleq$ that is generic with respect to dense sets definable in $\langle V,\in\rangle$.

For this, let us consider first the case where the worldly cardinal $\kappa$ has countable cofinality. In this case, we can find an increasing sequence $\kappa_n$ cofinal in $\kappa$, such that each $\kappa_n$ is $\Sigma_n$-correct in $V_\kappa$, meaning $V_{\kappa_n}\prec_{\Sigma_n}V_\kappa$.

In this case, we can build a definably generic filter $G$ for $\P$ in a sequence of stages. At stage $n$, we can find a well order up to $\kappa_n$ that meets all $\Sigma_n$ definable dense classes using parameters less than $V_{\kappa_n}$. The reason is that for any such definable dense set, we can meet it below $\kappa_n$ using the $\Sigma_n$-correctness of $\kappa_n$, and so by considering various parameters in turn, we can altogether handle all parameters below $V_{\kappa_n}$ using $\Sigma_n$ definitions. That is, the $n$th stage is itself an iteration of length $\kappa_n$, but it will meet all $\Sigma_n$ definable dense sets using parameters in $V_{\kappa_n}$.

Next, we observe that the ultimate well-order of $V_\kappa$ that arises from this construction after all stages is fully definably generic, since any definition with arbitrary parameters in $V_\kappa$ is a $\Sigma_n$ definition with parameters in $V_{\kappa_n}$ for some large enough $n$, and so we get a definably generic well order $\slantleq$. Therefore, the usual forcing argument shows that we get GBC in the resulting model $\langle V_\kappa,\in,\text{Def}(V_\kappa)\rangle$, as desired.

The remaining case occurs when kappa has uncountable cofinality. In this case, there is a club set $C\subseteq\kappa$ of ordinals $\gamma\in C$ with $V_\gamma\prec V_\kappa$. (We can just intersect the clubs $C_n$ of the $\Sigma_n$-correct cardinals.) Now, we build a well-order of $V_\kappa$ that is definably generic for every $V_\gamma$ for $\gamma\in C$. At limits, this is free, since every definable dense set in V_lambda with parameters below is also definable in some earlier $V_\gamma$. So it just reduces to the successor case, which we can get by the arguments above (or by induction). The next correct cardinal $\gamma$ above any ordinal has countable cofinality, since if one considers the next $\Sigma_1$-correct cardinal, the next $\Sigma_2$-correct cardinal, and so on, the limit will be fully correct and cofinality $\omega$.

The conclusion is that every worldly cardinal $\kappa$ admits a definably generic global well-order on $V_\kappa$ and therefore also admits a Gödel-Bernays GBC set theory structure $\langle V_\kappa,\in,X\rangle$, including the axiom of global choice.

The argument relativizes to any particular amenable class $A\subseteq V_\kappa$. Namely, if $\langle V_\kappa,\in,A\rangle$ is a model of $\text{ZFC}(A)$, then there is a definably generic well order $\slantleq$ of $V_\kappa$ such that $\langle V_\kappa,\in,A,\slantleq\rangle$ is a model of $\text{ZFC}(A,\slantleq)$, and so by taking the classes definable from $A$ and $\slantleq$, we get a GBC structure $X$ including both $A$ and $\slantleq$.

This latter observation will be put to good use in connection with Emma’s work on the Tarski’s revenge axiom, in regard to finding the optimal consistency strength for one of the principles.

Set theory with abundant urelements, STUK 10, Oxford, June 2023

Posted on by
Reply

This will be a talk for the Set Theory in the UK, STUK 10, held in Oxford 14 June 2023, organized by my students Clara List, Emma Palmer, and Wojciech Wołoszyn.

Abstract. I shall speak on the surprising strength of the second-order reflection principle in the context of set theory with abundant urelements. The theory GBcU with the abundant urelement axiom and second-order reflection is bi-interpretable with a strengthening of KM with a supercompact cardinal. This is joint work with Bokai Yao.

Lecture-notes-Set-theory-with-abundant-atoms-Oxford-STUK-2023Download

Reflection in second-order set theory with abundant urelements bi-interprets a supercompact cardinal

Posted on by
1

[bibtex key=”HamkinsYao:Reflection-in-second-order-set-theory-with-abundant-urelements”]

Download pdf at arXiv:2204.09766

Abstract. After reviewing various natural bi-interpretations in urelement set theory, including second-order set theories with urelements, we explore the strength of second-order reflection in these contexts. Ultimately, we prove, second-order reflection with the abundant atom axiom is bi-interpretable and hence also equiconsistent with the existence of a supercompact cardinal. The proof relies on a reflection characterization of supercompactness, namely, a cardinal $\kappa$ is supercompact if and only if every $\Pi^1_1$ sentence true in a structure $M$ (of any size) containing $\kappa$ in a language of size less than $\kappa$ is also true in a substructure $m\prec M$ of size less than $\kappa$ with $m\cap\kappa\in\kappa$.

See also my talk at the CUNY Set Theory Seminar: The surprising strength of reflection in second-order set theory with abundant urelements

The surprising strength of reflection in second-order set theory with abundant urelements, CUNY Set Theory seminar, April 2022

Posted on by
5

This was an online talk 15 April 12:15 for the CUNY Set Theory Seminar. Held on Zoom at 876 9680 2366.

Abstract. I shall give a general introduction to urelement set theory and the role of the second-order reflection principle in second-order urelement set theory GBCU and KMU. With the abundant atom axiom, asserting that the class of urelements greatly exceeds the class of pure sets, the second-order reflection principle implies the existence of a supercompact cardinal in an interpreted model of ZFC. The proof uses a reflection characterization of supercompactness: a cardinal $\kappa$ is supercompact if and only if for every second-order sentence $\psi$ true in some structure $M$ (of any size) in a language of size less than $\kappa$ is also true in a first-order elementary substructure $m\prec M$ of size less than $\kappa$. This is joint work with Bokai Yao.

See the article at: Reflection in second-order set theory with abundant urelements bi-interprets a supercompact cardinal

Determinacy for proper class games, Seminaire de Logique Lyon-Paris, April 2021

Posted on by
3

This will be a talk for the Seminaire de Logique Lyon-Paris on 14 April 2021 4pm Paris time (3pm UK). The talk will be held on Zoom at
875 1148 7359.

Abstract. The principle of open determinacy for class games — two-player games of perfect information with plays of length ω, where the moves are chosen from a possibly proper class, such as games on the ordinals — is not provable in Zermelo-Fraenkel set theory ZFC or Gödel-Bernays set theory GBC, if these theories are consistent, because provably in ZFC there is a definable open proper class game with no definable winning strategy. In fact, the principle of open determinacy and even merely clopen determinacy for class games implies Con(ZFC) and iterated instances Con(Con(ZFC)) and more, because it implies that there is a satisfaction class for first-order truth, and indeed a transfinite tower of truth predicates $\text{Tr}_\alpha$ for iterated truth-about-truth, relative to any class parameter. This is perhaps explained, in light of the Tarskian recursive definition of truth, by the more general fact that the principle of clopen determinacy is exactly equivalent over GBC to the principle of elementary transfinite recursion ETR over well-founded class relations. Meanwhile, the principle of open determinacy for class games is strictly stronger, although it is provable in the stronger theory GBC+$\Pi^1_1$-comprehension, a proper fragment of Kelley-Morse set theory KM.

Determinacy-of-proper-class-games-Paris-Lyon-2021Download

Kelley-Morse set theory does not prove the class Fodor principle

Posted on by
Reply
    1. [bibtex key=”GitmanHamkinsKaragila:KM-set-theory-does-not-prove-the-class-Fodor-theorem”]

Abstract.
We show that Kelley-Morse (KM) set theory does not prove the class Fodor principle, the assertion that every regressive class function $F:S\to\newcommand\Ord{\text{Ord}}\Ord$ defined on a stationary class $S$ is constant on a stationary subclass. Indeed, it is relatively consistent with KM for any infinite $\lambda$ with $\omega\leq\lambda\leq\Ord$ that there is a class function $F:\Ord\to\lambda$ that is not constant on any stationary class. Strikingly, it is consistent with KM that there is a class $A\subseteq\omega\times\Ord$, such that each section $A_n=\{\alpha\mid (n,\alpha)\in A\}$ contains a class club, but $\bigcap_n A_n$ is empty. Consequently, it is relatively consistent with KM that the class club filter is not $\sigma$-closed.

The class Fodor principle is the assertion that every regressive class function $F:S\to\Ord$ defined on a stationary class $S$ is constant on a stationary subclass of $S$. This statement can be expressed in the usual second-order language of set theory, and the principle can therefore be sensibly considered in the context of any of the various second-order set-theoretic systems, such as Gödel-Bernays (GBC) set theory or Kelley-Morse (KM) set theory. Just as with the classical Fodor’s lemma in first-order set theory, the class Fodor principle is equivalent, over a weak base theory, to the assertion that the class club filter is normal. We shall investigate the strength of the class Fodor principle and try to find its place within the natural hierarchy of second-order set theories. We shall also define and study weaker versions of the class Fodor principle.

If one tries to prove the class Fodor principle by adapting one of the classical proofs of the first-order Fodor’s lemma, then one inevitably finds oneself needing to appeal to a certain second-order class-choice principle, which goes beyond the axiom of choice and the global choice principle, but which is not available in Kelley-Morse set theory. For example, in one standard proof, we would want for a given $\Ord$-indexed sequence of non-stationary classes to be able to choose for each member of it a class club that it misses. This would be an instance of class-choice, since we seek to choose classes here, rather than sets. The class choice principle $\text{CC}(\Pi^0_1)$, it turns out, is sufficient for us to make these choices, for this principle states that if every ordinal $\alpha$ admits a class $A$ witnessing a $\Pi^0_1$-assertion $\varphi(\alpha,A)$, allowing class parameters, then there is a single class $B\subseteq \Ord\times V$, whose slices $B_\alpha$ witness $\varphi(\alpha,B_\alpha)$; and the property of being a class club avoiding a given class is $\Pi^0_1$ expressible.

Thus, the class Fodor principle, and consequently also the normality of the class club filter, is provable in the relatively weak second-order set theory $\text{GBC}+\text{CC}(\Pi^0_1)$. This theory is known to be weaker in consistency strength than the theory $\text{GBC}+\Pi^1_1$-comprehension, which is itself strictly weaker in consistency strength than KM.

But meanwhile, although the class choice principle is weak in consistency strength, it is not actually provable in KM; indeed, even the weak fragment $\text{CC}(\Pi^0_1)$ is not provable in KM. Those results were proved several years ago by the first two authors, but they can now be seen as consequences of the main result of this article (see corollary 15. In light of that result, however, one should perhaps not have expected to be able to prove the class Fodor principle in KM.

Indeed, it follows similarly from arguments of the third author in his dissertation that if $\kappa$ is an inaccessible cardinal, then there is a forcing extension $V[G]$ with a symmetric submodel $M$ such that $V_\kappa^M=V_\kappa$, which implies that $\mathcal M=(V_\kappa,\in, V^M_{\kappa+1})$ is a model of Kelley-Morse, and in $\mathcal M$, the class Fodor principle fails in a very strong sense.

In this article, adapting the ideas of Karagila to the second-order set-theoretic context and using similar methods as in Gitman and Hamkins’s previous work on KM, we shall prove that every model of KM has an extension in which the class Fodor principle fails in that strong sense: there can be a class function $F:\Ord\to\omega$, which is not constant on any stationary class. In particular, in these models, the class club filter is not $\sigma$-closed: there is a class $B\subseteq\omega\times\Ord$, each of whose vertical slices $B_n$ contains a class club, but $\bigcap B_n$ is empty.

Main Theorem. Kelley-Morse set theory KM, if consistent, does not prove the class Fodor principle. Indeed, if there is a model of KM, then there is a model of KM with a class function $F:\Ord\to \omega$, which is not constant on any stationary class; in this model, therefore, the class club filter is not $\sigma$-closed.

We shall also investigate various weak versions of the class Fodor principle.

Definition.

  1. For a cardinal $\kappa$, the class $\kappa$-Fodor principle asserts that every class function $F:S\to\kappa$ defined on a stationary class $S\subseteq\Ord$ is constant on a stationary subclass of $S$.
  2. The class ${<}\Ord$-Fodor principle is the assertion that the $\kappa$-class Fodor principle holds for every cardinal $\kappa$.
  3. The bounded class Fodor principle asserts that every regressive class function $F:S\to\Ord$ on a stationary class $S\subseteq\Ord$ is bounded on a stationary subclass of $S$.
  4. The very weak class Fodor principle asserts that every regressive class function $F:S\to\Ord$ on a stationary class $S\subseteq\Ord$ is constant on an unbounded subclass of $S$.

We shall separate these principles as follows.

Theorem. Suppose KM is consistent.

  1. There is a model of KM in which the class Fodor principle fails, but the class ${<}\Ord$-Fodor principle holds.
  2. There is a model of KM in which the class $\omega$-Fodor principle fails, but the bounded class Fodor principle holds.
  3. There is a model of KM in which the class $\omega$-Fodor principle holds, but the bounded class Fodor principle fails.
  4. $\text{GB}^-$ proves the very weak class Fodor principle.

Finally, we show that the class Fodor principle can neither be created nor destroyed by set forcing.

Theorem. The class Fodor principle is invariant by set forcing over models of $\text{GBC}^-$. That is, it holds in an extension if and only if it holds in the ground model.

Let us conclude this brief introduction by mentioning the following easy negative instance of the class Fodor principle for certain GBC models. This argument seems to be a part of set-theoretic folklore. Namely, consider an $\omega$-standard model of GBC set theory $M$ having no $V_\kappa^M$ that is a model of ZFC. A minimal transitive model of ZFC, for example, has this property. Inside $M$, let $F(\kappa)$ be the least $n$ such that $V_\kappa^M$ fails to satisfy $\Sigma_n$-collection. This is a definable class function $F:\Ord^M\to\omega$ in $M$, but it cannot be constant on any stationary class in $M$, because by the reflection theorem there is a class club of cardinals $\kappa$ such that $V_\kappa^M$ satisfies $\Sigma_n$-collection.

Read more by going to the full article: [bibtex key=”GitmanHamkinsKaragila:KM-set-theory-does-not-prove-the-class-Fodor-theorem”]

 

 

Kelley-Morse set theory does not prove the class Fodor Principle, CUNY Set Theory Seminar, March, 2019

Posted on by
1
This will be talk for the CUNY Set Theory seminar, Friday, March 22, 2019, 10 am in room 6417 at the CUNY Graduate Center.
Abstract. I shall discuss recent joint work with Victoria Gitman and Asaf Karagila, in which we proved that Kelley-Morse set theory (which includes the global choice principle) does not prove the class Fodor principle, the assertion that every regressive class function $F:S\to\text{Ord}$ defined on a stationary class $S$ is constant on a stationary subclass. Indeed, it is relatively consistent with KM for any infinite $\lambda$ with $\omega\leq\lambda\leq\text{Ord}$ that there is a class function $F:\text{Ord}\to\lambda$ that is not constant on any stationary class. Strikingly, it is consistent with KM that there is a sequence of classes $A_n$, each containing a class club, but the intersection of all $A_n$ is empty. Consequently, it is relatively consistent with KM that the class club filter is not $\sigma$-closed.
I am given to understand that the talk will be streamed live online. I’ll post further details when I have them.

Open class determinacy is preserved by forcing

Posted on by
Reply

[bibtex key=”HamkinsWoodin2018:Open-class-determinacy-is-preserved-by-forcing”]

Abstract. The principle of open class determinacy is preserved by pre-tame class forcing, and after such forcing, every new class well-order is isomorphic to a ground-model class well-order. Similarly, the principle of elementary transfinite recursion ETR${}_\Gamma$ for a fixed class well-order $\Gamma$ is preserved by pre-tame class forcing. The full principle ETR itself is preserved by countably strategically closed pre-tame class forcing, and after such forcing, every new class well-order is isomorphic to a ground-model class well-order. Meanwhile, it remains open whether ETR is preserved by all forcing, including the forcing merely to add a Cohen real.

 

The principle of elementary transfinite recursion ETR — according to which every first-order class recursion along any well-founded class relation has a solution — has emerged as a central organizing concept in the hierarchy of second-order set theories from Gödel-Bernays set theory GBC up to Kelley-Morse set theory KM and beyond. Many of the principles in the hierarchy can be seen as asserting that certain class recursions have solutions.

In addition, many of these principles, including ETR and its variants, are equivalently characterized as determinacy principles for certain kinds of class games. Thus, the hierarchy is also fruitfully unified and organized by determinacy ideas.

This hierarchy of theories is the main focus of study in the reverse mathematics of second-order set theory, an emerging subject aiming to discover the precise axiomatic principles required for various arguments and results in second-order set theory. The principle ETR itself, for example, is equivalent over GBC to the principle of clopen determinacy for class games and also to the existence of iterated elementary truth predicates (see Open determinacy for class games); since every clopen game is also an open game, the principle ETR is naturally strengthened by the principle of open determinacy for class games, and this is a strictly stronger principle (see Hachtman and Sato); the weaker principle ETR${}_\text{Ord}$, meanwhile, asserting solutions to class recursions of length Ord, is equivalent to the class forcing theorem, which asserts that every class forcing notion admits a forcing relation, to the existence of set-complete Boolean completions of any class partial order, to the existence of Ord-iterated elementary truth predicates, to the determinacy of clopen games of rank at most Ord+1, and to other natural set-theoretic principles (see The exact strength of the class forcing theorem).

Since one naturally seeks in any subject to understand how one’s fundamental principles and tools interact, we should like in this article to consider how these second-order set-theoretic principles are affected by forcing. These questions originated in previous work of Victoria Gitman and myself, and question 1 also appears in the dissertation of Kameryn Williams, which was focused on the structure of models of second-order set theories.

It is well-known, of course, that ZFC, GBC, and KM are preserved by set forcing and by tame class forcing, and this is true for other theories in the hierarchy, such as GBC$+\Pi^1_n$-comprehension and higher levels of the second-order comprehension axiom. The corresponding forcing preservation theorem for ETR and for open class determinacy, however, has not been known.

Question 1. Is ETR preserved by forcing?

Question 2. Is open class determinacy preserved by forcing?

We intend to ask in each case about class forcing as well as set forcing. Question 1 is closely connected with the question of whether forcing can create new class well-order order types, longer than any class well-order in the ground model. Specifically, Victoria Gitman and I had observed earlier that ETR${}_\Gamma$ for a specific class well-order $\Gamma$ is preserved by pre-tame class forcing, and this would imply that the full principle ETR would also be preserved, if no fundamentally new class well-orders are created by the forcing. In light of the fact that forcing over models of ZFC adds no new ordinals, that would seem reasonable, but proof is elusive, and the question remains open. Can forcing add new class well-orders, perhaps very tall ones that are not isomorphic to any ground model class well-order? Perhaps there are some very strange models of GBC that gain new class well-order order types in a forcing extension.

Question 3. Assume GBC. After forcing, must every new class well-order be isomorphic to a ground-model class well-order? Does ETR imply this?

The main theorem of this article provides a full affirmative answer to question 2, and partial affirmative answers to questions 2 and 3.

Main Theorem.

  1. Open class determinacy is preserved by pre-tame class forcing. After such forcing, every new class well-order is isomorphic to a ground-model class well-order.
  2. The principle ETR${}_\Gamma$, for any fixed class well order $\Gamma$, is preserved by pre-tame class forcing.
  3. The full principle ETR is preserved by countably strategically closed pre-tame class forcing. After such forcing, every new class well-order is isomorphic to a ground-model class well-order.

We should like specifically to highlight the fact that questions 1 and 3 remain open even in the case of the forcing to add a Cohen real. Is ETR preserved by the forcing to add a Cohen real? After adding a Cohen real, is every new class well-order isomorphic to a ground-model class well-order? One naturally expects affirmative answers, especially in a model of ETR.

For more, click through the arxiv for a pdf of the full article.

[bibtex key=”HamkinsWoodin2018:Open-class-determinacy-is-preserved-by-forcing”]

Kameryn J. Williams, PhD 2018, CUNY Graduate Center

Posted on by
Reply

Kameryn J. Williams successfully defended his dissertation under my supervision at the CUNY Graduate Center on April 6th, 2018, earning his Ph.D. degree in May 2018. He has accepted a position in mathematics at the University of Hawaii, to begin Fall 2018.

What a pleasure it was to work with Kameryn, an extremely talented mathematician with wide interests and huge promise.

Kameryn J Williams | MathOverflow | ar$\chi$iv

Kameryn J. Williams, The Structure of Models of Second-order Set Theories,  Ph.D. dissertation for The Graduate Center of the City University of New York, May, 2018. arXiv:1804.09526.

Abstract. This dissertation is a contribution to the project of second-order set theory, which has seen a revival in recent years. The approach is to understand second-order set theory by studying the structure of models of second-order set theories. The main results are the following, organized by chapter. First, I investigate the poset of T-realizations of a fixed countable model of ZFC, where T is a reasonable second-order set theory such as GBC or KM, showing that it has a rich structure. In particular, every countable partial order embeds into this structure. Moreover, we can arrange so that these embedding preserve the existence/nonexistence of upper bounds, at least for finite partial orders. Second I generalize some constructions of Marek and Mostowski from KM to weaker theories. They showed that every model of KM plus the Class Collection schema “unrolls” to a model of ZFC− with a largest cardinal. I calculate the theories of the unrolling for a variety of second-order set theories, going as weak as GBC + ETR. I also show that being T-realizable goes down to submodels for a broad selection of second-order set theories T. Third, I show that there is a hierarchy of transfinite recursion principles ranging in strength from GBC to KM. This hierarchy is ordered first by the complexity of the properties allowed in the recursions and second by the allowed heights of the recurions. Fourth, I investigate the question of which second-order set theories have least models. I show that strong theories—such as KM or $\Pi^1_1$-CA—do not have least transitive models, while weaker theories—from GBC to GBC + ETR${}_{\text{Ord}}$—do have least transitive models.

In addition to his dissertation work and the research currently arising out of it, Kameryn has undertaken a number of collaborations with various international research efforts, including the following:

  • He is a co-author on The exact strength of the class forcing theorem. [bibtex key=”GitmanHamkinsHolySchlichtWilliams:The-exact-strength-of-the-class-forcing-theorem”]
  • He is co-author on a current joint project with Miha Habič, myself, Daniel Klausner and Jonathan Verner concerning the nonamalgamation phenomenon in the generic multiverse of a countable model of set theory.
  • He is co-author on a current joint project with myself and Philip Welch concerning the universal $\Sigma_1$-definable finite sequence, an analogue of the universal finite set, but for the constructible universe.

 

On the strengths of the class forcing theorem and clopen class game determinacy, Prague set theory seminar, January 2018

Posted on by
1

This will be a talk for the Prague set theory seminar, January 24, 11:00 am to about 2pm (!).

Abstract. The class forcing theorem is the assertion that every class forcing notion admits corresponding forcing relations. This assertion is not provable in Zermelo-Fraenkel ZFC set theory or Gödel-Bernays GBC set theory, if these theories are consistent, but it is provable in stronger second-order set theories, such as Kelley-Morse KM set theory. In this talk, I shall discuss the exact strength of this theorem, which turns out to be equivalent to the principle of elementary transfinite recursion ETRord for class recursions on the ordinals. The principle of clopen determinacy for class games, in contrast, is strictly stronger, equivalent over GBC to the full principle of ETR for class recursions over arbitrary class well-founded relations. These results and others mark the beginnings of the emerging subject I call the reverse mathematics of second-order set theory.

The exact strength of the class forcing theorem | Open determinacy for class games

Second-order transfinite recursion is equivalent to Kelley-Morse set theory over GBC

Posted on by
Reply

1167px-Wooden_spiral_stairs_(Nebotičnik,_Ljubljana)_croped
A few years ago, I had observed after hearing a talk by Benjamin Rin that the principle of first-order transfinite recursion for set well-orders is equivalent to the replacement axiom over Zermelo set theory, and thus we may take transfinite recursion as a fundamental set-theoretic principle, one which yields full ZFC when added to Zermelo’s weaker theory (plus foundation).

In later work, Victoria Gitman and I happened to prove that the principle of elementary transfinite recursion ETR, which allows for first-order class recursions along proper class well-orders (not necessarily set-like) is equivalent to the principle of determinacy for clopen class games [1]. Thus, once again, a strong recursion principle exhibited robustness as a fundamental set-theoretic principle.

The theme continued in recent joint work on the class forcing theorem, in which Victoria Gitman, myself, Peter Holy, Philipp Schlicht and Kameryn Williams [2] proved that the principle $\text{ETR}_{\text{Ord}}$, which allows for first-order class recursions of length $\text{Ord}$, is equivalent to twelve natural set-theoretic principles, including the existence of forcing relations for class forcing notions, the existence of Boolean completions for class partial orders, the existence of various kinds of truth predicates for infinitary logics, the existence of $\text{Ord}$-iterated truth predicates, and to the principle of determinacy for clopen class games of rank at most $\text{Ord}+1$.

A few days ago, a MathOverflow question of Alec Rhea’s — Is there a stronger form of recursion? — led me to notice that one naturally gains additional strength by pushing the recursion principles further into second-order set theory.

So let me introduce the second-order recursion principle STR and make the comparatively simple observation that over Gödel-Bernays GBC set theory this is equivalent to Kelley-Morse set theory KM. Thus, we may take this kind of recursion as a fundamental set-theoretic principle.

Definition. In the context of second-order set theory, the principle of second-order transfinite recursion, denoted STR, asserts of any formula $\varphi$ in the second-order language of set theory, that if $\Gamma=\langle I,\leq_\Gamma\rangle$ is any class well-order and $Z$ is any class parameter, then there is a class $S\subset I\times V$ that is a solution of the recursion, in the sense that
$$S_i=\{\ x\ \mid\  \varphi(x,S\upharpoonright i,Z)\ \}$$
for every $i\in I$, where where $S_i=\{\ x\ \mid\ (i,x)\in S\ \}$ is the section on coordinate $i$ and where $S\upharpoonright i=\{\ (j,x)\in S\ \mid\ j<_\Gamma i\ \}$ is the part of the solution at stages below $i$ with respect to $\Gamma$.

Theorem. The principle of second-order transfinite recursion STR is equivalent over GBC to the second-order comprehension principle. In other words, GBC+STR is equivalent to KM.

Proof. Kelley-Morse set theory proves that every second-order recursion has a solution in the same way that ZFC proves that every set-length well-ordered recursion has a solution. Namely, we simply consider the classes which are partial solutions to the recursion, in that they obey the recursive requirement, but possibly only on an initial segment of the well-order $\Gamma$. We may easily show by induction that any two such partial solutions agree on their common domain (this uses second-order comprehension in order to find the least point of disagreement, if any), and we can show that any given partial solution, if not already a full solution, can be extended to a partial solution on a strictly longer initial segment. Finally, we show that the common values of all partial solutions is therefore a solution of the recursion. This final step uses second-order comprehension in order to define what the common values are for the partial solutions to the recursion.

Conversely, the principle of second-order transfinite recursion clearly implies the second-order comprehension axiom, by considering recursions of length one. For any second-order assertion $\varphi$ and class parameter $Z$, we may deduce that $\{x\mid \varphi(x,Z)\}$ is a class, and so the second-order class comprehension principle holds. $\Box$

It is natural to consider various fragments of STR, such as $\Sigma^1_n\text{-}\text{TR}_\Gamma$, which is the assertion that every $\Sigma^1_n$-formula $\varphi$ admits a solution for recursions of length $\Gamma$.  Such principles are provable in proper fragments of KM, since for a given level of complexity, we only need a corresponding fragment of comprehension to undertake the proof that the recursion has a solution. The full STR asserts $\Sigma^1_\omega\text{-}\text{TR}$, allowing any length. The theorem shows that STR is equivalent to recursions of length $1$, since once you get the second-order comprehension principle, then you get solutions for recursions of any length. Thus, with second-order transfinite recursion, a little goes a long way. Perhaps it is more natural to think of transfinite recursion in this context not as axiomatizing KM, since it clearly implies second-order comprehension straight away, but rather as an apparent strengthening of KM that is actually provable in KM. This contrasts with the first-order situation of ETR with respect to GBC, where GBC+ETR does make a proper strengthening of GBC.

  1. [bibtex key=”GitmanHamkins2016:OpenDeterminacyForClassGames”]
  2. [bibtex key=”GitmanHamkinsHolySchlichtWilliams:The-exact-strength-of-the-class-forcing-theorem”]
Photo by Petar Milošević (Own work) [CC BY-SA 4.0], via Wikimedia Commons

Regula Krapf, Ph.D. 2017, University of Bonn

Posted on by
4

Regula Krapf successfully defended her PhD dissertation January 12, 2017 at the University of Bonn, with a dissertation entitled, “Class forcing and second-order arithmetic.”  I was a member of the dissertation examining committee. Peter Koepke was the dissertation supervisor.

Regula Krapf

Regula Krapf, Class forcing and second-order arithmetic, dissertation 2017, University of Bonn. (Slides)

Abstract. We provide a framework in a generalization of Gödel-Bernays set theory for performing class forcing. The forcing theorem states that the forcing relation is a (definable) class in the ground model (definability lemma) and that every statement that holds in a class-generic extension is forced by a condition in the generic filter (truth lemma). We prove both positive and negative results concerning the forcing theorem. On the one hand, we show that the definability lemma for one atomic formula implies the forcing theorem for all formulae in the language of set theory to hold. Furthermore, we introduce several properties which entail the forcing theorem. On the other hand, we give both counterexamples to the definability lemma and the truth lemma. In set forcing, the forcing theorem can be proved for all forcing notions by constructing a unique Boolean completion. We show that in class forcing the existence of a Boolean completion is essentially equivalent to the forcing theorem and, moreover, Boolean completions need not be unique.

The notion of pretameness was introduced to characterize those forcing notions which preserve the axiom scheme of replacement. We present several new characterizations of pretameness in terms of the forcing theorem, the preservation of separation, the existence of nice names for sets of ordinals and several other properties. Moreover, for each of the aforementioned properties we provide a corresponding characterization of the Ord-chain condition.

Finally, we prove two equiconsistency results which compare models of ZFC (with large cardinal properties) and models of second-order arithmetic with topological regularity properties (and determinacy hypotheses). We apply our previous results on class forcing to show that many important arboreal forcing notions preserve the $\Pi^1_1$-perfect set property over models of second-order arithmetic and also give an example of a forcing notion which implies the $\Pi^1_1$-perfect set property to fail in the generic extension.

Regula has now taken up a faculty position at the University of Koblenz.

Open determinacy for games on the ordinals is stronger than ZFC, CUNY Logic Workshop, October 2015

Posted on by
1

This will be a talk for the CUNY Logic Workshop on October 2, 2015.

Abstract. The principle of open determinacy for class games — two-player games of perfect information with plays of length $\omega$, where the moves are chosen from a possibly proper class, such as games on the ordinals — is not provable in Zermelo-Fraenkel set theory ZFC or Gödel-Bernays set theory GBC, if these theories are consistent, because provably in ZFC there is a definable open proper class game with no definable winning strategy. In fact, the principle of open determinacy and even merely clopen determinacy for class games implies Con(ZFC) and iterated instances Con(Con(ZFC)) and more, because it implies that there is a satisfaction class for first-order truth, and indeed a transfinite tower of truth predicates $\text{Tr}_\alpha$ for iterated truth-about-truth, relative to any class parameter. This is perhaps explained, in light of the Tarskian recursive definition of truth, by the more general fact that the principle of clopen determinacy is exactly equivalent over GBC to the principle of elementary transfinite recursion ETR over well-founded class relations. Meanwhile, the principle of open determinacy for class games is provable in the stronger theory GBC+$\Pi^1_1$-comprehension, a proper fragment of Kelley-Morse set theory KM.

This is joint work with Victoria Gitman, with the helpful participation of Thomas Johnstone.

Related article and posts:

 

 

Open determinacy for class games

Posted on by
7

[bibtex key=GitmanHamkins2016:OpenDeterminacyForClassGames]

Abstract. The principle of open determinacy for class games — two-player games of perfect information with plays of length $\omega$, where the moves are chosen from a possibly proper class, such as games on the ordinals — is not provable in Zermelo-Fraenkel set theory ZFC or Godel-Bernays set theory GBC, if these theories are consistent, because provably in ZFC there is a definable open proper class game with no definable winning strategy. In fact, the principle of open determinacy and even merely clopen determinacy for class games implies Con(ZFC) and iterated instances Con(Con(ZFC)) and more, because it implies that there is a satisfaction class for first-order truth, and indeed a transfinite tower of truth predicates $\text{Tr}_\alpha$ for iterated truth-about-truth, relative to any class parameter. This is perhaps explained, in light of the Tarskian recursive definition of truth, by the more general fact that the principle of clopen determinacy is exactly equivalent over GBC to the principle of transfinite recursion over well-founded class relations. Meanwhile, the principle of open determinacy for class games is provable in the stronger theory GBC$+\Pi^1_1$-comprehension, a proper fragment of Kelley-Morse set theory KM.

See my earlier posts on part of this material:

 

Open determinacy for proper class games implies Con(ZFC) and much more

Posted on by
5

1000px-Apollonian_gasket.svg

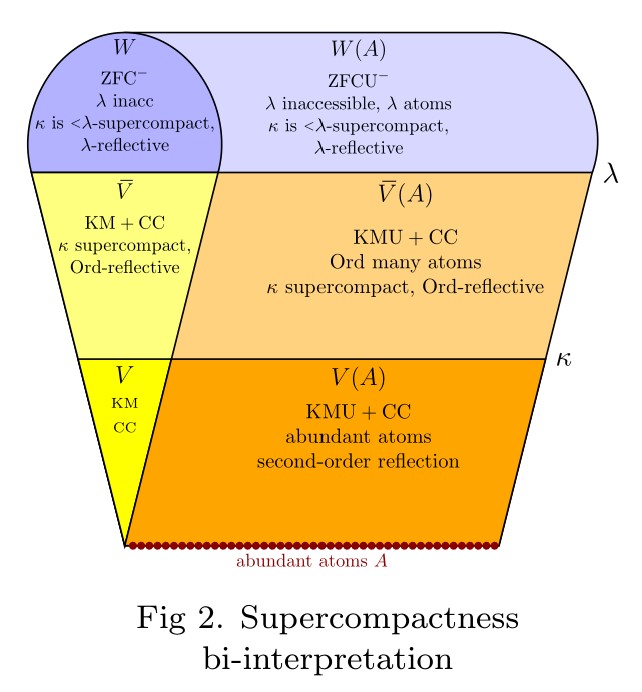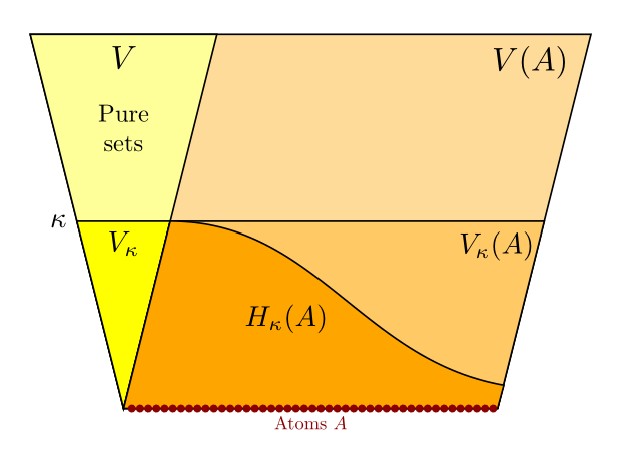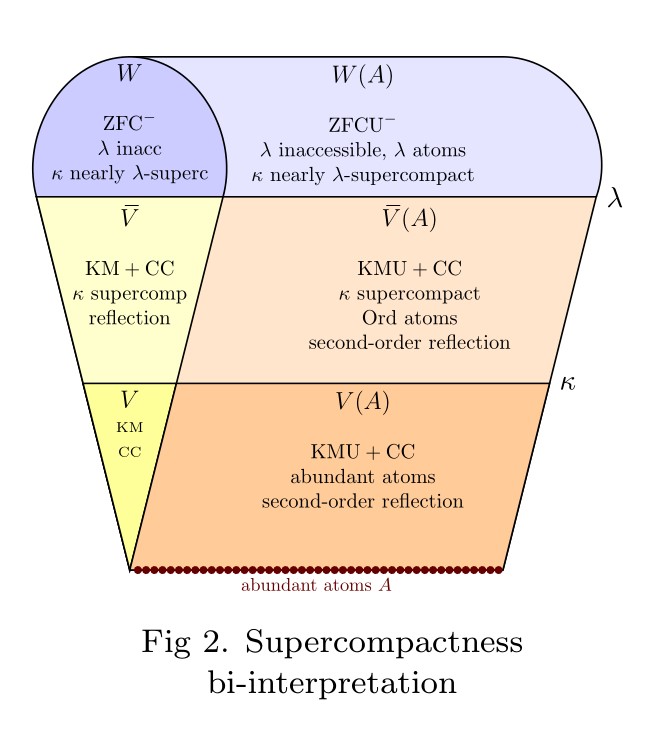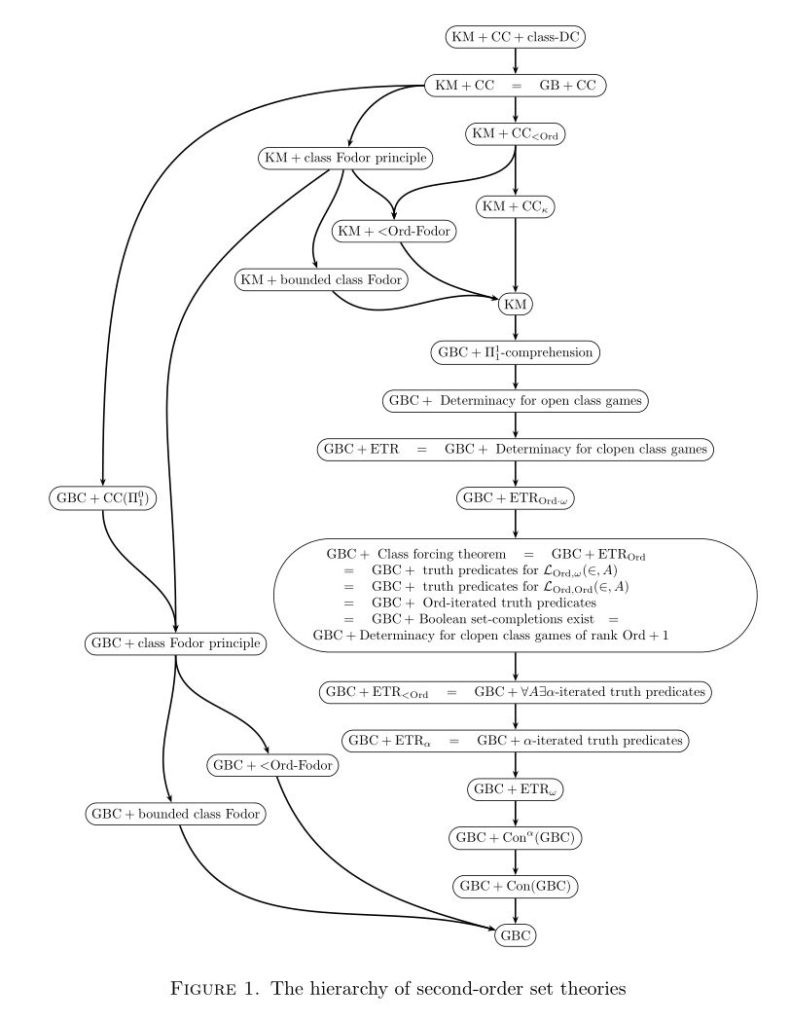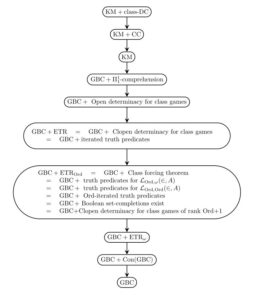
$\newcommand\Tr{\text{Tr}}$One of the intriguing lessons we have learned in the past half-century of set-theoretic developments is that there is a surprisingly robust connection between infinitary game theory and fundamental set-theoretic principles, including large cardinals. Assertions about the existence of strategies in infinite games often turn out to have an unexpected set-theoretic power. In this post, I should like to give another specific example of this, which Thomas Johnstone and I hit upon yesterday in an enjoyable day of mathematics.

Specifically, I’d like to prove that if we generalize the open-game concept from sets to classes, then assuming consistency, ZFC cannot prove that every definable open class game is determined, and indeed, over Gödel-Bernays set theory GBC the principle of open determinacy (and even just clopen determinacy) implies Con(ZFC) and much more.

To review a little, we are talking about games of perfect information, where two players alternately play elements from an allowed space $X$ of possible moves, and together they build an infinite sequence $\vec x=\langle x_0,x_1,x_2,\ldots\rangle$ in $X^\omega$, which is the resulting play of this particular instance of the game. We have a fixed collection of plays $A\subset X^\omega$ that is used to determine the winner, namely, the first player wins this particular instance of the game if the resulting play $\vec x$ is in $A$, and otherwise the second player wins. A strategy for a player is a function $\sigma:X^{<\omega}\to X$, which tells a player how to move next, given a finite position in the game. Such a strategy is winning for that player, if he or she always wins by following the instructions, no matter how the opponent plays. The game is determined, if one of the players has a winning strategy.

It is a remarkable but elementary fact that if the winning condition $A$ is an open set, then the game is determined. One can prove this by using the theory of ordinal game values, and my article on transfinite game values in infinite chess contains an accessible introduction to the theory of game values. Basically, one defines that a position has game value zero (for player I, say), if the game has already been won at that stage, in the sense that every extension of that position is in the winning payoff set $A$. A position with player I to play has value $\alpha+1$, if player I can move to a position with value $\alpha$, and $\alpha$ is minimal. The value of a position with player II to play is the supremum of the values of all the positions that he or she might reach in one move, provided that those positions have a value. The point now is that if a position has a value, then player I can play so as strictly to decrease the value, and player II cannot play so as to increase it. So if a position has a value, then player I has a winning strategy, which is the value-reducing strategy. Conversely, if a position does not have a value, then player II can maintain that fact, and player I cannot play so as to give it a value; thus, in this case player II has a winning strategy, the value-maintaining strategy. Thus, we have proved the Gale-Stewart theorem: every open game is determined.

That proof relied on the space of moves $X$ being a set, since we took a supremum over the values of the possible moves, and if $X$ were a proper class, we couldn’t be sure to stay within the class of ordinals and the recursive procedure might break down. What I’d like to do is to consider more seriously the case where $X$ is a proper class. Similarly, we allow the payoff collection $A$ to be a proper class, and the strategies $\sigma:X^{<\omega}\to X$ are also proper classes. Can we still prove the Gale-Steward theorem for proper classes? The answer is no, unless we add set-theoretic strength. Indeed, even clopen determinacy has set-theoretic strength.

Theorem. (GBC) Clopen determinacy for proper classes implies Con(ZFC) and much more. Specifically, there is a clopen game, such the existence of a winning strategy is equivalent to the existence of a satisfaction class for first-order truth.

Proof. Let me first describe a certain open game, the truth-telling game, with those features, and I shall later modify it to a clopen game. The truth-telling game will have two players, which I call the challenger and the truth-teller. At any point in the game, the challenger plays by making an inquiry about a particular set-theoretic formula $\varphi(\vec a)$ with parameters. The truth-teller must reply to the inquiry by stating either true or false, and in the case that the formula $\varphi$ is an existential assertion $\exists x\,\psi(x,\vec a)$ declared to be true, then the truth teller must additionally identify a particular witness $b$ and assert that $\psi(b,\vec a)$ is true. So a play of the game consists of a sequence of such inquires and replies.

The truth-teller wins a play of the game, provided that she never violates the recursive Tarskian truth conditions. Thus, faced with an atomic formula, she must state true or false in accordance with the actual truth or falsity of that atomic formula, and similarly,
she must say true to $\varphi\wedge\psi$ just in case she said true to both $\varphi$ and $\psi$ separately (if those formulas had been issued by the challeger), and she must state opposite truth values for $\varphi$ and $\neg\varphi$, if both are issued as challenges.

This is an open game, since the challenger will win, if at all, at a finite stage of play, when the violation of the Tarskian truth conditions is first exhibited.

Lemma 1. The truth-teller has a winning strategy in the truth-telling game if and only if there is a satisfaction class for first-order truth.

Proof. Clearly, if there is a satisfaction class for first-order truth, then the truth-teller has a winning strategy, which is simply to answer all questions about truth by consulting the
satisfaction class. Since that class obeys the Tarskian conditions, she will win the game, no matter which challenges are issued.

Conversely, suppose that the truth-teller has a winning strategy $\tau$ in the game. I claim that we may use $\tau$ to build a satisfaction class for first-order truth. Specifically, let $T$ be the collection of formulas $\varphi(\vec a)$ that are asserted to be true by $\tau$ in any play according to $\tau$. I claim that $T$ is a satisfaction class. We may begin by noting that since $T$ must correctly state the truth of all atomic formulas, it follows that the particular answers that $\tau$ gives on the atomic formulas does not depend on the order of the challenges issued by the challenger. Now, we argue by induction on formulas that the truth values issued by $\tau$ does not depend on the order of the challenges. For example, if all plays in which $\varphi(\vec a)$ is issued as a challenge come out true, then all plays in which $\neg\varphi(\vec a)$ is challenged will result in false, or else we would have a play in which $\tau$ would violate the Tarskian truth conditions. Similarly, if $\varphi$ and $\psi$ always come out the same way, then so does $\varphi\wedge\psi$. We don’t claim that $\tau$ must always issue the same witness $b$ for an existential $\exists x\,\psi(x,\vec a)$, but if it ever says true to this statement, then it will provide some witness $b$, and for that statement $\psi(b,\vec a)$, the truth value stated by $\tau$ is independent of the order of play by the challenger, by induction. Thus, by induction on formulas, the answers provided by the truth-teller strategy $\tau$ gives us a satisfaction predicate for first-order truth. QED

Lemma 2. The challenger has no winning strategy in the truth-telling game.

Proof. Suppose that $F$ is a strategy for the challenger. So $F$ is a proper class function that directs the challenger to issue certain challenges, given the finite sequence of previous challenges and truth-telling answers. By the reflection theorem, there is a closed unbounded proper class of cardinals $\theta$, such that $F”V_\theta\subset V_\theta$. That is, $V_\theta$ is closed under $F$, in the sense that if all previous challenges and responses come from $V_\theta$, then the next challenge will also come from $V_\theta$. Since $\langle V_\theta,\in\rangle$ is a set, we have a satisfaction predicate on it. Consider the play, where the truth-teller replies to all inquires by consulting truth in $V_\theta$, rather than truth in $V$. The point is that if the challenger follows $\tau$, then all the inquiries will involve only parameters $\vec a$ in $V_\theta$, provided that the truth-teller also always gives witnesses in $V_\theta$, which in this particular play will be the case. Since the satisfaction predicate on $V_\theta$ does satisfy the Tarskian truth conditions, it follows that the truth-teller will win this instance of the game, and so $F$ is not a winning strategy for the challenger. QED

Thus, if open determinacy holds for classes, then there is a satisfaction predicate for first-order truth.

This implies Con(ZFC) for reasons I explained on my post KM implies Con(ZFC) and much more, by appealing to the fact that we have the collection axiom relative to the class for the satisfaction predicate itself, and this is enough to verify that the nonstandard instances of collection also must be declared true in the satisfaction predicate.

But so far, we only have an open game, rather than a clopen game, since the truth-teller wins only by playing the game out for infinitely many steps. So let me describe how to modify the game to be clopen. Specifically, consider the version of the truth-telling game, where the challenger must also state on each move a specific ordinal $\alpha_n$, which descend during play $\alpha_0>\alpha_1>\cdots>\alpha_n$. If the challenger gets to $0$, then the truth-teller is declared the winner. For this modified game, the winner is known in finitely many moves, because either the truth-teller violates the Tarskian conditions or the challenger hits zero. So this is a clopen game. Since we made the game harder for the challenger, it follows that the challenger still can have no winning strategy. One can modify the proof of lemma 1 to say that if $\tau$ is a winning strategy for the truth teller, then the truth assertions made by $\tau$ in response to all plays with sufficiently large ordinals for the challenger all agree with one another independently of the order of the formulas issued by the challenger. Thus, there is a truth-telling strategy just in case there is a satisfaction class for first-order truth.

So clopen determinacy for class games implies the existence of a satisfaction class for first-order truth, and this implies Con(ZFC) and much more. QED

One may easily modify the game by allowing a fixed class parameter $B$, so that clopen determinacy implies that there is a satisfaction class relative to truth in $\langle V,\in,B\rangle$.

Furthermore, we may also get iterated truth predicates. Specifically, consider the iterated truth-telling game, which in addition to the usual language of set theory, we have a hierarchy of predicates $\Tr_\alpha$ for any ordinal $\alpha$. We now allow the challenger to ask about formulas in this expanded language, and the truth teller is required to obey not only the usual Tarskian recursive truth conditions, but also the requirements that $\Tr_\alpha(\varphi(\vec a))$ is declared true just in case $\varphi(\vec a)$ uses only truth predicates $\Tr_\beta$ for $\beta<\alpha$ and also $\varphi(\vec a)$ is declared true (if this challenge was issued).

The main arguments as above generalize easily to show that the challenger cannot have a winning strategy in this iterated truth-telling game, and the truth-teller has a strategy just in case there is a satisfaction predicate for truth-about-truth iterated through the ordinals.  Thus, the principle of open determinacy for proper class games implies Con(Con(ZFC)) and $\text{Con}^\alpha(\text{ZFC})$ and so on.

Let me finish by mentioning that Kelley-Morse set theory is able to prove open determinacy for proper class games in much the same manner as we proved the Gale-Stewart theorem above, using well-ordered class meta-ordinals, rather than merely set ordinals, as well as in other ways. If there is interest, I can make a further post about that, so just ask in the comments!