Tag Archives: forcing

Forcing is simply the iterative conception undertaken with multivalued logic, ForcingFest, Oslo, June 2024

Posted on by
Reply

I shall be speaking at the ForcingFest meeting at the University of Oslo, 21 June 2024.

Abstract. I will explain how the forcing construction can be seen as a direct implementation of the iterative conception, giving rise to the cumulative hierarchy, but undertaken in the context of multivalued logic. The shape of the logic that is available in effect enables a certain constructive interference of the truth values in such a way that can affect the truth judgements. The core utility of forcing arises from the fact that we can often control these consequences by making a careful choice of the logic to be used, thereby controlling the truth values even of natural set-theoretic statements such as the continuum hypothesis.

Slides-ForcingFest-Oslo-Hamkins-June-2024Download

The computable model theory of forcing, Rutgers Logic Seminar, December 2023

Posted on by
Reply

This will be a talk for the Rutgers University Logic Seminar, December 4, 2023.

Abstract. I shall discuss the computable model theory of forcing. To what extent can we view forcing as a computational process on the models of set theory? Given an oracle for the atomic or elementary diagram of a model (M,∈M) of set theory, for example, there are senses in which one may compute M-generic filters G⊂ℙ∈M over that model and compute the diagrams of the corresponding forcing extensions M[G]. Meanwhile, no such computational process is functorial, for there must always be isomorphic alternative presentations of the same model of set theory that lead by the computational process to non-isomorphic forcing extensions. Indeed, there is no Borel function providing generic filters that is functorial in this sense. This is joint work with myself, Russell Miller and Kameryn Williams.

The paper is available on the arxiv at https://arxiv.org/abs/2007.00418.

Set-theoretic forcing as a computational process, Midwest Computability Seminar, Chicago, May 2023

Posted on by
5

This is a talk for the MidWest Computability Seminar conference held May 2, 2023 at the University of Chicago. The talk will be available via Zoom at https://notredame.zoom.us/j/99754332165?pwd=RytjK1RFZU5KWnZxZ3VFK0g4YTMyQT09.

Abstract: I shall explore several senses in which set-theoretic forcing can be seen as a computational process on the models of set theory. Given an oracle for the atomic or elementary diagram of a model (M,∈M) of set theory, for example, there are senses in which one may compute M-generic filters G⊂ℙ∈M over that model and compute the diagrams of the corresponding forcing extensions M[G]. Meanwhile, no such computational process is functorial, for there must always be isomorphic alternative presentations of the same model of set theory that lead by the computational process to non-isomorphic forcing extensions. Indeed, there is no Borel function providing generic filters that is functorial in this sense. This is joint work with myself, Russell Miller and Kameryn Williams.

The paper is available on the arxiv at https://arxiv.org/abs/2007.00418.

The talk took place in “The Barn” in the upper space between the Reyerson Laboratory and Eckhart Hall, where the University of Chicago Department of Mathematics is located:

Slides-Forcing-as-a-computational-process-MCS-Chicago-2023Download

A survey of set-theoretic geology, Notre Dame Logic Seminar, January 2023

Posted on by
Reply

This will be a talk 31 January 2-3 for the Notre Dame Logic Seminar.

Abstract. I shall give a general introduction and account of the main elements of set-theoretic geology, the motivating questions, the central definitions, and the main results, including newer advances. We’ll discuss ground models, the ground axiom, the mantle, the ground-model definability theorem, Usuba’s results on downward directedness and more. 

Pseudo-countable models

Posted on by
Reply

[bibtex key=”Hamkins:Pseudo-countable-models”]

Download pdf at arXiv:2210.04838

Abstract. Every mathematical structure has an elementary extension to a pseudo-countable structure, one that is seen as countable inside a suitable class model of set theory, even though it may actually be uncountable. This observation, proved easily with the Boolean ultrapower theorem, enables a sweeping generalization of results concerning countable models to a rich realm of uncountable models. The Barwise extension theorem, for example, holds amongst the pseudo-countable models—every pseudo-countable model of ZF admits an end extension to a model of ZFC+V=L. Indeed, the class of pseudo-countable models is a rich multiverse of set-theoretic worlds, containing elementary extensions of any given model of set theory and closed under forcing extensions and interpreted models, while simultaneously fulfilling the Barwise extension theorem, the Keisler-Morley theorem, the resurrection theorem, and the universal finite sequence theorem, among others.

The sentence asserting its own non-forceability by nontrivial forcing

Posted on by
Reply

At the meeting here in Konstanz, Giorgo Venturi and I considered the sentence $\sigma$, which asserts its own non-forceability by nontrivial forcing. That is, $\sigma$ asserts that there is no nontrivial forcing notion forcing $\sigma$. $$\sigma\quad\iff\quad \neg\exists\mathbb{B}\ \Vdash_{\mathbb{B}}\sigma.$$ The sentence $\sigma$ would be a fixed-point of the predicate for not being nontrivially forceable.

In any model of set theory $V$ in which $\sigma$ is true, then in light of what it asserts, it would not be forceable by nontrivial forcing, and so it would be false in all nontrivial forcing extensions of that model $V[G]$. And in any model $W$ where it is false, then because of what it asserts, it would be nontrivially forceable, and so it would be true in some forcing extension of that model $W[G]$.

But this is a contradiction! It cannot ever be true, since if it were true in $V$, it would have to be false in all extensions $V[G]$, and therefore true in some subsequent extension $V[G][H]$. But that model is a forcing extension of $V$, contradicting the claim that it is false in all such extensions.

So it must always be false, but this can’t happen, since then in any given model, in light of what it asserts, it would have to be true. So it cannot ever be true or false.

Conclusion: there is no such sentence σ that asserts its own nontrivial forceability. This is no fixed-point for not being nontrivially forceable.

But doesn’t this contradict the fixed-point lemma? After all, the fixed-point lemma shows that we can produce fixed points for any expressible assertion.

The resolution of the conundrum is that although for any given assertion $\varphi$, we can express “$\varphi$ is forceable”, we cannot express “x is the Gödel code of a forceable sentence”, for reasons similar to those for Tarski’s theorem on the nondefinability of truth.

Therefore, we are not actually in a situation to apply the fixed-point lemma. And ultimately the argument shows that there can be no sentence $\sigma$ that asserts “$\sigma$ is not forceable by nontrivial forcing”.

Ultimately, I find the logic of this sentence $\sigma$, asserting its own non-nontrivial forceability, to be a set-theoretic forcing analogue of the Yablo paradox. The sentence holds in a model of set theory whenever it fails in all subsequent models obtained by forcing, and that relation is exactly what arises in the Yablo paradox.

Forcing as a computational process, Kobe Set Theory Workshop, March 2021

Posted on by
Reply

This was a talk for the Kobe Set Theory Workshop, held on the occasion of Sakaé Fuchino’s retirement, 9-11 March 2021.

Abstract. I shall discuss senses in which set-theoretic forcing can be seen as a computational process on the models of set theory. Given an oracle for the atomic or elementary diagram of a model of set theory $\langle M,\in^M\rangle$, for example, one may in various senses compute $M$-generic filters $G\subset P\in M$ and the corresponding forcing extensions $M[G]$. Meanwhile, no such computational process is functorial, for there must always be isomorphic alternative presentations of the same model of set theory $M$ that lead by the computational process to non-isomorphic forcing extensions $M[G]\not\cong M[G’]$. Indeed, there is no Borel function providing generic filters that is functorial in this sense.

This is joint work with Russell Miller and Kameryn Williams.

Forcing-as-a-computational-process-Kobe-2021 SlidesDownload

Forcing as a computational process

[bibtex key=”HamkinsMillerWilliams:Forcing-as-a-computational-process”]

Forcing as a computational process

Posted on by
2

[bibtex key=”HamkinsMillerWilliams:Forcing-as-a-computational-process”]

Abstract. We investigate how set-theoretic forcing can be seen as a computational process on the models of set theory. Given an oracle for information about a model of set theory $\langle M,\in^M\rangle$, we explain senses in which one may compute $M$-generic filters $G\subseteq\mathbb{P}\in M$ and the corresponding forcing extensions $M[G]$. Specifically, from the atomic diagram one may compute $G$, from the $\Delta_0$-diagram one may compute $M[G]$ and its $\Delta_0$-diagram, and from the elementary diagram one may compute the elementary diagram of $M[G]$. We also examine the information necessary to make the process functorial, and conclude that in the general case, no such computational process will be functorial. For any such process, it will always be possible to have different isomorphic presentations of a model of set theory $M$ that lead to different non-isomorphic forcing extensions $M[G]$. Indeed, there is no Borel function providing generic filters that is functorial in this sense.

Forcing as a computational process, Cambridge, Februrary 2019

Posted on by
4

This will be a talk for Set Theory in the United Kingdom (STUK 1), to be held in the other place, February 16, 2019.

Abstract. We investigate the senses in which set-theoretic forcing can be seen as a computational process on the models of set theory. Given an oracle for the atomic or elementary diagram of a model of set theory $\langle M,\in^M\rangle$, for example, we explain senses in which one may compute $M$-generic filters $G\subset P\in M$ and the corresponding forcing extensions $M[G]$. Meanwhile, no such computational process is functorial, for there must always be isomorphic alternative presentations of the same model of set theory $M$ that lead by the computational process to non-isomorphic forcing extensions $M[G]\not\cong M[G’]$. Indeed, there is no Borel function providing generic filters that is functorial in this sense.

This is joint work with Russell Miller and Kameryn Williams.

The rearrangement number: how many rearrangements of a series suffice to validate absolute convergence? Warwick Mathematics Colloquium, October 2018

Posted on by
2

This will be a talk for the Mathematics Colloquium at the University of Warwick, to be held October 19, 2018, 4:00 pm in Lecture Room B3.02 at the Mathematics Institute. I am given to understand that the talk will be followed by a wine and cheese reception.Abstract. The Riemann rearrangement theorem asserts that a series $\sum_n a_n$ is absolutely convergent if and only if every rearrangement $\sum_n a_{p(n)}$ of it is convergent, and furthermore, any conditionally convergent series can be rearranged so as to converge to any desired extended real value. How many rearrangements $p$ suffice to test for absolute convergence in this way? The rearrangement number, a new cardinal characteristic of the continuum, is the smallest size of a family of permutations, such that whenever the convergence and value of a convergent series is invariant by all these permutations, then it is absolutely convergent. The exact value of the rearrangement number turns out to be independent of the axioms of set theory. In this talk, I shall place the rearrangement number into a discussion of cardinal characteristics of the continuum, including an elementary introduction to the continuum hypothesis and an account of Freiling’s axiom of symmetry.

This talk is based in part on joint work with Andreas Blass, Will Brian, myself, Michael Hardy and Paul Larson.

Set-theoretic blockchains

Posted on by
1

[bibtex key=”HabicHamkinsKlausnerVernerWilliams2018:Set-theoretic-blockchains”]

Abstract. Given a countable model of set theory, we study the structure of its generic multiverse, the collection of its forcing extensions and ground models, ordered by inclusion. Mostowski showed that any finite poset embeds into the generic multiverse while preserving the nonexistence of upper bounds. We obtain several improvements of his result, using what we call the blockchain construction to build generic objects with varying degrees of mutual genericity. The method accommodates certain infinite posets, and we can realize these embeddings via a wide variety of forcing notions, while providing control over lower bounds as well. We also give a generalization to class forcing in the context of second-order set theory, and exhibit some further structure in the generic multiverse, such as the existence of exact pairs.

A question in set-theoretic geology: if $M[G][K]=M[H][K],$ then can we conlude $M[G]=M[H]$?

Posted on by
4

I was recently asked this interesting question on set-theoretic geology by Iian Smythe, a set-theory post-doc at Rutgers University; the problem arose in the context of one of this current research projects.

Question. Assume that two product forcing extensions are the same $$M[G][K]=M[H][K],$$ where $M[G]$ and $M[H]$ are forcing extensions of $M$ by the same forcing notion $\mathbb{P}$, and $K\subset\mathbb{Q}\in M$ is both $M[G]$ and $M[H]$-generic with respect to this further forcing $\mathbb{Q}$.  Can we conclude that $$M[G]=M[H]\ ?$$ Can we make this conclusion at least in the special case that $\mathbb{P}$ is adding a Cohen real and $\mathbb{Q}$ is collapsing the continuum?

It seems natural to hope for a positive answer, because we are aware of many such situations that arise with forcing, where indeed $M[G]=M[H]$. Nevertheless, the answer is negative. Indeed, we cannot legitimately make this conclusion even when both steps of forcing are adding merely a Cohen real. And such a counterexample implies that there is a counterexample of the type mentioned in the question, simply by performing further collapse forcing.

Theorem. For any countable model $M$ of set theory, there are $M$-generic Cohen reals $c$, $d$ and $e$, such that

  1. The Cohen reals $c$ and $e$ are mutually generic over $M$.
  2. The Cohen reals $d$ and $e$ are mutually generic over $M$.
  3. These two pairs produce the same forcing extension $M[c][e]=M[d][e]$.
  4. But  the intermediate models are different $M[c]\neq M[d]$.

Proof. Fix $M$, and let $c$ and $e$ be any two mutually generic Cohen reals over $M$. Let us view them as infinite binary sequences, that is, as elements of Cantor space. In the extension $M[c][e]$, let $d=c+e \mod 2$, in each coordinate. That is, we get $d$ from $c$ by flipping bits, but only on coordinates that are $1$ in $e$. This is the same as applying a bit-flipping automorphism of the forcing, which is available in $M[e]$, but not in $M$. Since $c$ is $M[e]$-generic by reversing the order of forcing, it follows that $d$ also is $M[e]$-generic, since the automorphism is in $M[e]$. Thus, $d$ and $e$ are mutually generic over $M$. Further, $M[c][e]=M[d][e]$, because $M[e][c]=M[e][d]$, as $c$ and $d$ were isomorphic generic filters by an isomorphism in $M[e]$. But finally, $M[c]$ and $M[d]$ are not the same, because from $c$ and $d$ together we can construct $e$, because we can tell exactly which bits were flipped. $\Box$

If one now follows the $e$ forcing with collapse forcing, one achieves a counterexample model of the type mentioned in the question, namely, with $M[c][e*K]=M[d][e*K]$, but $M[c]\neq M[d]$.

I have a feeling that my co-authors on a current paper in progress, Set-theoretic blockchains, on the topic of non-amalgamation in the generic multiverse, will tell me that the argument above is an instance of some of the theorems we prove in the latter part of that paper. (Miha, please tell me in the comments, if you see this, or tell me where I have seen this argument before; I think I made this argument or perhaps seen it before.) The paper is [bibtex key=”HabicHamkinsKlausnerVernerWilliams2018:Set-theoretic-blockchains”].

Open class determinacy is preserved by forcing

Posted on by
Reply

[bibtex key=”HamkinsWoodin2018:Open-class-determinacy-is-preserved-by-forcing”]

Abstract. The principle of open class determinacy is preserved by pre-tame class forcing, and after such forcing, every new class well-order is isomorphic to a ground-model class well-order. Similarly, the principle of elementary transfinite recursion ETR${}_\Gamma$ for a fixed class well-order $\Gamma$ is preserved by pre-tame class forcing. The full principle ETR itself is preserved by countably strategically closed pre-tame class forcing, and after such forcing, every new class well-order is isomorphic to a ground-model class well-order. Meanwhile, it remains open whether ETR is preserved by all forcing, including the forcing merely to add a Cohen real.

 

The principle of elementary transfinite recursion ETR — according to which every first-order class recursion along any well-founded class relation has a solution — has emerged as a central organizing concept in the hierarchy of second-order set theories from Gödel-Bernays set theory GBC up to Kelley-Morse set theory KM and beyond. Many of the principles in the hierarchy can be seen as asserting that certain class recursions have solutions.

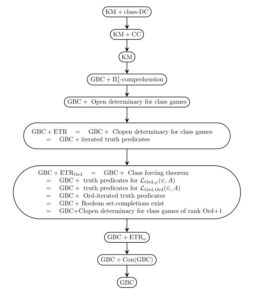
In addition, many of these principles, including ETR and its variants, are equivalently characterized as determinacy principles for certain kinds of class games. Thus, the hierarchy is also fruitfully unified and organized by determinacy ideas.

This hierarchy of theories is the main focus of study in the reverse mathematics of second-order set theory, an emerging subject aiming to discover the precise axiomatic principles required for various arguments and results in second-order set theory. The principle ETR itself, for example, is equivalent over GBC to the principle of clopen determinacy for class games and also to the existence of iterated elementary truth predicates (see Open determinacy for class games); since every clopen game is also an open game, the principle ETR is naturally strengthened by the principle of open determinacy for class games, and this is a strictly stronger principle (see Hachtman and Sato); the weaker principle ETR${}_\text{Ord}$, meanwhile, asserting solutions to class recursions of length Ord, is equivalent to the class forcing theorem, which asserts that every class forcing notion admits a forcing relation, to the existence of set-complete Boolean completions of any class partial order, to the existence of Ord-iterated elementary truth predicates, to the determinacy of clopen games of rank at most Ord+1, and to other natural set-theoretic principles (see The exact strength of the class forcing theorem).

Since one naturally seeks in any subject to understand how one’s fundamental principles and tools interact, we should like in this article to consider how these second-order set-theoretic principles are affected by forcing. These questions originated in previous work of Victoria Gitman and myself, and question 1 also appears in the dissertation of Kameryn Williams, which was focused on the structure of models of second-order set theories.

It is well-known, of course, that ZFC, GBC, and KM are preserved by set forcing and by tame class forcing, and this is true for other theories in the hierarchy, such as GBC$+\Pi^1_n$-comprehension and higher levels of the second-order comprehension axiom. The corresponding forcing preservation theorem for ETR and for open class determinacy, however, has not been known.

Question 1. Is ETR preserved by forcing?

Question 2. Is open class determinacy preserved by forcing?

We intend to ask in each case about class forcing as well as set forcing. Question 1 is closely connected with the question of whether forcing can create new class well-order order types, longer than any class well-order in the ground model. Specifically, Victoria Gitman and I had observed earlier that ETR${}_\Gamma$ for a specific class well-order $\Gamma$ is preserved by pre-tame class forcing, and this would imply that the full principle ETR would also be preserved, if no fundamentally new class well-orders are created by the forcing. In light of the fact that forcing over models of ZFC adds no new ordinals, that would seem reasonable, but proof is elusive, and the question remains open. Can forcing add new class well-orders, perhaps very tall ones that are not isomorphic to any ground model class well-order? Perhaps there are some very strange models of GBC that gain new class well-order order types in a forcing extension.

Question 3. Assume GBC. After forcing, must every new class well-order be isomorphic to a ground-model class well-order? Does ETR imply this?

The main theorem of this article provides a full affirmative answer to question 2, and partial affirmative answers to questions 2 and 3.

Main Theorem.

  1. Open class determinacy is preserved by pre-tame class forcing. After such forcing, every new class well-order is isomorphic to a ground-model class well-order.
  2. The principle ETR${}_\Gamma$, for any fixed class well order $\Gamma$, is preserved by pre-tame class forcing.
  3. The full principle ETR is preserved by countably strategically closed pre-tame class forcing. After such forcing, every new class well-order is isomorphic to a ground-model class well-order.

We should like specifically to highlight the fact that questions 1 and 3 remain open even in the case of the forcing to add a Cohen real. Is ETR preserved by the forcing to add a Cohen real? After adding a Cohen real, is every new class well-order isomorphic to a ground-model class well-order? One naturally expects affirmative answers, especially in a model of ETR.

For more, click through the arxiv for a pdf of the full article.

[bibtex key=”HamkinsWoodin2018:Open-class-determinacy-is-preserved-by-forcing”]

Nonamalgamation in the Cohen generic multiverse, CUNY Logic Workshop, March 2018

Posted on by
Reply

This will be a talk for the CUNY Logic Workshop on March 23, 2018, GC 6417 2-3:30pm.

Abstract. Consider a countable model of set theory $M$ in the context of all its successive forcing extensions and grounds. This generic multiverse has long been known to exhibit instances of nonamalgamation: one can have two extensions $M[c]$ and $M[d]$, both adding a merely a generic Cohen real, which have no further extension in common. In this talk, I shall describe new joint work that illuminates the extent of non-amalgamation: every finite partial order (and more) embeds into the generic multiverse over any given model in a way that preserves amalgamability and non-amalgamability. The proof uses the set-theoretic blockchain argument (pictured above), which has affinities with constructions in computability theory in the Turing degrees. Other arguments, which also resemble counterparts in computability theory, show that the generic multiverse exhibits the exact pair phenonemon for increasing chains. This is joint work with Miha Habič, myself, Lukas Daniel Klausner and Jonathan Verner. The paper will be available this Spring.

https://plus.google.com/u/0/+JoelDavidHamkins1/posts/NJp2N7bkkrR

Corey Switzer, The Cichoń Diagram for Degrees of Relative Constructibility

Posted on by
1

My student Corey Switzer has just completed a paper:


Corey Switzer, The Cichoń Diagram for Degrees of Relative Constructibility, ArXiv e-print:1801.06497.

 

Abstract. Following a line of research initiated in Brendle/Brooke-Taylor/Ng/Nies, I describe a general framework for turning reduction concepts of relative computability into diagrams forming an analogy with the Cichoń diagram for cardinal characteristics of the continuum. I show that working from relatively modest assumptions about a notion of reduction, one can construct a robust version of such a diagram. As an application, I define and investigate the Cichoń Diagram for degrees of constructibility relative to a fixed inner model W. Many analogies hold with the classical theory as well as some surprising differences. Along the way I introduce a new axiom stating, roughly, that the constructibility diagram is as complex as possible.

This interesting paper concerns a generalization of the Cichoń diagram to arbitrary reducibility notions, focussing on the case of the constructibility degrees, or somewhat more generally, relative constructibility $\leq_W$ over a fixed inner model $W$.

The classes are defined by an abstract generalization of the ideas underlying the familiar cardinal characteristics and the classical Cichoń diagram. Namely, $B_{\leq}(R)$ is the set of reals that $\leq$-build a witness for the fact that the reals of $W$ are small with respect to the relation $R$, that is, an $R$-bound for the reals of $W$; and $D_{\leq}(R)$ is the set of reals that $\leq$-build a witness for the fact that the reals of $W$ are not big with respect to the relation $R$, that is, a real that is not $R$-dominated by any real in $W$.

These classes fit together in a way that forms a robust analogy with the classical Cichoń diagram.

In his paper, Corey proves that the diagram is complete with respect to the inclusions indicated, by analyzing the nature of the diagram in various forcing extensions of $W$, such as the following.

 

In the end, he shows that in a suitable (proper) forcing extension, one can achieve all the separations simultaneously.

Indeed, the assertion that all separations are attained can be taken as a set-theoretic principle or axiom of its own, the complete Cichoń diagram assertion CD. He proves, for example, that CD is a consequence of the maximality principle.

See Corey’s blog post about his paper.