This will be a talk for the Seminar on Frontier Issues in Logic and Philosophy
The First Forum on Logic and Philosophy
逻辑与哲学前沿问题研究”学术研讨会暨第一届逻辑与哲学论坛
Changchun, China, 18-20 July 2025

Pointwise definable end-extensions of models of arithmetic and set theory
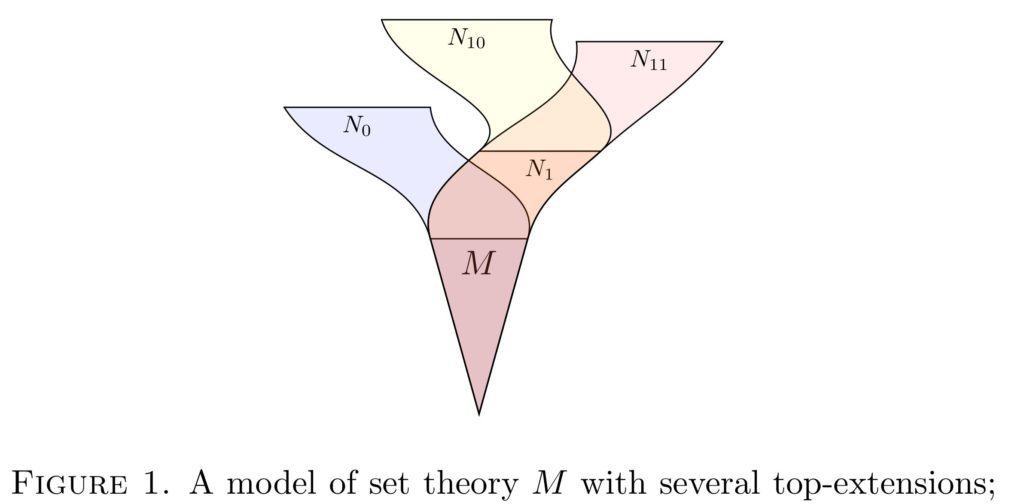
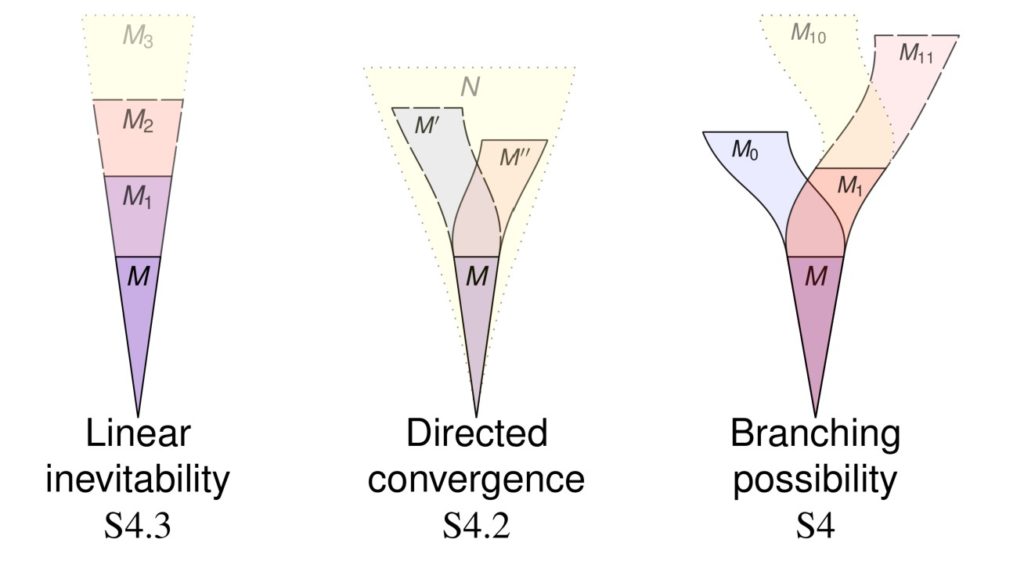
Abstract. The existence of pointwise definable models of set theory offers a fundamental engagement with what has become known as the Math Tea argument, according to which there must be undefinable real numbers, since there are only countable many definitions, but uncountably many real numbers. I shall present a new flexible model-theoretic method showing that every countable model of Peano Arithmetic (PA) admits a pointwise definable end-extension, one in which every object is definable without parameters. The argument makes a fundamental use of the universal algorithm. Also, any model of PA of size at most continuum admits an extension that is Leibnizian, meaning that any two distinct points are separated by some expressible property. Similar results hold in set theory, where one can also achieve V=L in the extension, or indeed any suitable theory holding in an inner model of the original model.