 In set theory, we have the phenomenon of the universal definition. This is a property , first-order expressible in the language of set theory, that necessarily holds of exactly one set, but which can in principle define any particular desired set that you like, if one should simply interpret the definition in the right set-theoretic universe. So could be defining the set of real numbes or the integers or the number or a certain group or a certain topological space or whatever set you would want it to be. For any mathematical object , there is a set-theoretic universe in which is the unique object for which .
In set theory, we have the phenomenon of the universal definition. This is a property , first-order expressible in the language of set theory, that necessarily holds of exactly one set, but which can in principle define any particular desired set that you like, if one should simply interpret the definition in the right set-theoretic universe. So could be defining the set of real numbes or the integers or the number or a certain group or a certain topological space or whatever set you would want it to be. For any mathematical object , there is a set-theoretic universe in which is the unique object for which .
The universal definition can be viewed as a set-theoretic analogue of the universal algorithm, a topic on which I have written several recent posts:
Let’s warm up with the following easy instance.
Theorem. Any particular real number can become definable in a forcing extension of the universe.
Proof. By Easton’s theorem, we can control the generalized continuum hypothesis precisely on the regular cardinals, and if we start (by forcing if necessary) in a model of GCH, then there is a forcing extension where just in case the binary digit of is . In the resulting forcing extension , therefore, the real is definable as: the real whose binary digits conform with the GCH pattern on the cardinals . QED
Since this definition can be settled in a rank-initial segment of the universe, namely, , the complexity of the definition is . See my post on Local properties in set theory to see how I think about locally verifiable and locally decidable properties in set theory.
If we push the argument just a little, we can go beyond the reals.
Theorem. There is a formula , of complexity , such that for any particular object , there is a forcing extension of the universe in which defines .
Proof. Fix any set . By the axiom of choice, we may code with a set of ordinals for some cardinal . (One well-orders the transitive closure of and thereby finds a bijection for some , and then codes to a set by an ordinal pairing function. The set tells you , which tells you by the Mostowski collapse, and from this you find .) By Easton’s theorem, there is a forcing extension in which the GCH holds at all for a limit ordinal , but fails at , and such that just in case for . That is, we manipulate the GCH pattern to exactly code both and the elements of . Let assert that is the set that is decoded by this process: look for the first stage where the GCH fails at , and then extract the set of ordinals, and then check if is the set coded by . The assertion did not depend on , and since it can be verified in any sufficiently large , the assertion has complexity . QED
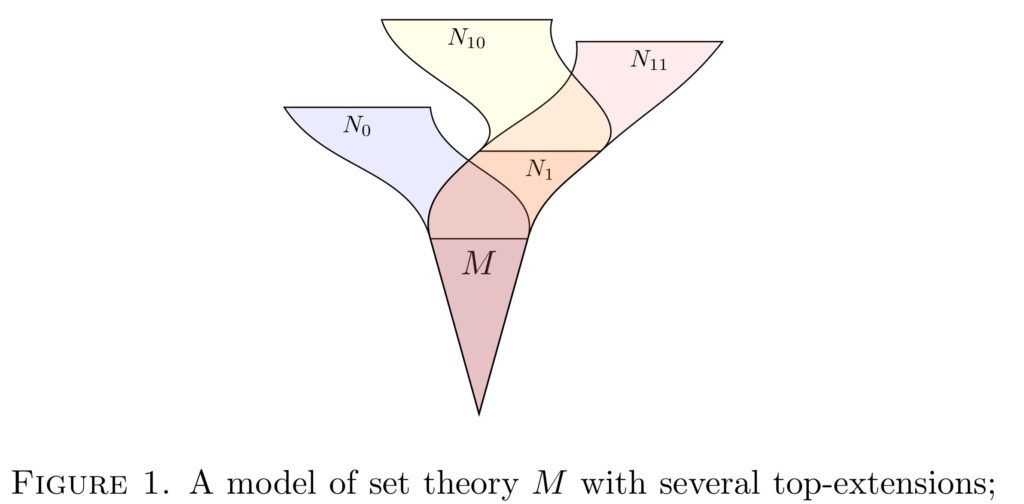
Let’s try to make a better universal definition. As I mentioned at the outset, I have been motivated to find a set-theoretic analogue of the universal algorithm, and in that computable context, we had a universal algorithm that could not only produce any desired finite set, when run in the right universe, but which furthermore had a robust interaction between models of arithmetic and their top-extensions: any set could be extended to any other set for which the algorithm enumerated it in a taller universe. Here, I’d like to achieve the same robustness of interaction with the universal definition, as one moves from one model of set theory to a taller model. We say that one model of set theory is a top-extension of another , if all the new sets of have rank totally above the ranks occuring in . Thus, is a rank-initial segment of . If there is a least new ordinal in , then this is equivalent to saying that .
Theorem. There is a formula , such that
- In any model of ZFC, there is a unique set satisfying .
- For any countable model and any , there is a top-extension of such that .
Thus, is the universal definition: it always defines some set, and that set can be any desired set, even when moving from a model to a top-extension .
Proof. The previous manner of coding will not achieve property 2, since the GCH pattern coding started immediately, and so it would be preserved to any top extension. What we need to do is to place the coding much higher in the universe, so that in the top extension , it will occur in the part of that is totally above .
But consider the following process. In any model of set theory, let assert that is the empty set unless the GCH holds at all sufficiently large cardinals, and indeed is false unless there is a cardinal and ordinal such that the GCH holds at all cardinals above . In this case, let be the smallest such cardinal for which that is true, and let be the smallest ordinal working with this . So both and are definable. Now, let be the set of ordinals for which the GCH holds at , and let assert that is the set coded by the set .
It is clear that defines a unique set, in any model of ZFC, and so (1) holds. For (2), suppose that is a countable model of ZFC and . It is a fact that every countable model of ZFC has a top-extension, by the definable ultrapower method. Let be a top extension of . Let be a forcing extension of in which the set is coded into the GCH pattern very high up, at cardinals totally above , and such that the GCH holds above this coding, in such a way that the process described in the previous paragraph would define exactly the set . So holds in , which is a top-extension of as no new sets of small rank are added by the forcing. So statement (2) also holds. QED
The complexity of the definition is , mainly because in order to know where to look for the coding, one needs to know the ordinals and , and so one needs to know that the GCH always holds above that level. This is a property, since it cannot be verified locally only inside some .
A stronger analogue with the universal algorithm — and this is a question that motivated my thinking about this topic — would be something like the following:
Question. Is there is a formula , that is, a locally verifiable property, with the following properties?
- In any model of ZFC, the class is a set.
- It is consistent with ZFC that is empty.
- In any countable model in which and any set with , then there is a top-extension of in which .
An affirmative answer would be a very strong analogue with the universal algorithm and Woodin’s theorem about which I wrote previously. The idea is that the properties in set theory are analogous to the computably enumerable properties in computability theory. Namely, to verify that an object has a certain computably enumerable property, we run a particular computable process and then sit back, waiting for the process to halt, until a stage of computation arrives at which the property is verified. Similarly, in set theory, to verify that a set has a particular property, we sit back watching the construction of the cumulative set-theoretic universe, until a stage arrives that provides verification of the property. This is why in statement (3) we insist that , since the properties are always upward absolute to top-extensions; once an object is placed into , then it will never be removed as one makes the universe taller.
So the hope was that we would be able to find such a universal definition, which would serve as a set-theoretic analogue of the universal algorithm used in Woodin’s theorem.
If one drops the first requirement, and allows to sometimes be a proper class, then one can achieve a positive answer as follows.
Theorem. There is a formula with the following properties.
- If the GCH holds, then is empty.
- For any countable model where and any with , there is a top extension of in which .
Proof. Let assert that the set is coded into the GCH pattern. We may assume that the coding mechanism of a set is marked off by certain kinds of failures of the GCH at odd-indexed alephs, with the pattern at intervening even-indexed regular cardinals forming the coding pattern. This is , since any large enough will reveal whether a given set is coded in this way. And because of the manner of coding, if the GCH holds, then no set is coded. Also, if the GCH holds eventually, then only a set-sized collection is coded. Finally, any countable model where only a set is coded can be top-extended to another model in which any desired superset of that set is coded. QED
Update. Originally, I had proposed an argument for a negative answer to the question, and I was actually a bit disappointed by that, since I had hoped for a positive answer. However, it now seems to me that the argument I had written is wrong, and I am grateful to Ali Enayat for his remarks on this in the comments. I have now deleted the incorrect argument.
Meanwhile, here is a positive answer to the question in the case of models of .
Theorem. There is a formula with the following properties:
- In any model of , the class is a set.
- It is relatively consistent with that is empty; indeed, in any model of , the class is empty.
- If thinks that is a set and is a larger set , then there is a top-extension of in which .
Proof. Let hold, if there is some ordinal such that every element of is coded into the GCH pattern below some cardinal , with as small as possible with that property, and is the next set coded into the GCH pattern above . This is a property, since it can be verified in any sufficiently large .
In any model of , there must be some sets that are no coded into the pattern, for if every set is coded that way then there would be a definable well-ordering of the universe and we would have . So in any model of , there is a bound on the ordinals for which exists, and therefore is a set. So statement (1) holds.
Statement (2) holds, because we may arrange it so that the GCH itself implies that no set is coded at all, and so would always fail.
For statement (3), suppose that and is countable. In , there must be some minimal rank for which there is a set of rank that is not coded into the GCH pattern. Let be an elementary top-extension of , so agrees that is that minimal rank. Now, by forcing over , we can arrange to code all the sets of rank into the GCH pattern above the height of the original model , and we can furthermore arrange so as to code any given element of just above that coding. And so on, we can iterate it so as to arrange the coding above the height of so that exactly the elements of now satisfy , but no more. In this way, we will ensure that , as desired. QED
I find the situation unusual, in that often results from the models-of-arithmetic context generalize to set theory with models of , because the global well-order means that models of have definable Skolem functions, which is true in every model of arithmetic and which sometimes figures implicitly in constructions. But here, we have the result of Woodin’s theorem generalizing from models of arithmetic to models of . Perhaps this suggests that we should expect a fully positive solution for models of set theory.
Further update. Woodin and I have now established the fully general result of the universal finite set, which subsumes much of the preliminary early analysis that I had earlier made in this post. Please see my post, The universal finite set.
 Abstract. Potentialism is the view, originating in the classical dispute between actual and potential infinity, that one’s mathematical universe is never fully completed, but rather unfolds gradually as new parts of it increasingly come into existence or become accessible or known to us. Recent work emphasizes the modal aspect of potentialism, while decoupling it from arithmetic and from infinity: the essence of potentialism is about approximating a larger universe by means of universe fragments, an idea that applies to set-theoretic as well as arithmetic foundations. The modal language and perspective allows one precisely to distinguish various natural potentialist conceptions in the foundations of mathematics, whose exact modal validities are now known. Ultimately, this analysis suggests a refocusing of potentialism on the issue of convergent inevitability in comparison with radical branching. I shall defend the theses, first, that convergent potentialism is implicitly actualist, and second, that we should understand ultrafinitism in modal terms as a form of potentialism, one with surprising parallels to the case of arithmetic potentialism.
Abstract. Potentialism is the view, originating in the classical dispute between actual and potential infinity, that one’s mathematical universe is never fully completed, but rather unfolds gradually as new parts of it increasingly come into existence or become accessible or known to us. Recent work emphasizes the modal aspect of potentialism, while decoupling it from arithmetic and from infinity: the essence of potentialism is about approximating a larger universe by means of universe fragments, an idea that applies to set-theoretic as well as arithmetic foundations. The modal language and perspective allows one precisely to distinguish various natural potentialist conceptions in the foundations of mathematics, whose exact modal validities are now known. Ultimately, this analysis suggests a refocusing of potentialism on the issue of convergent inevitability in comparison with radical branching. I shall defend the theses, first, that convergent potentialism is implicitly actualist, and second, that we should understand ultrafinitism in modal terms as a form of potentialism, one with surprising parallels to the case of arithmetic potentialism.








![King of Hearts / Wikimedia Commons / CC-BY-SA-3.0 [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons Empire_State_Building_New_York_March_2015](http://jdh.hamkins.org/wp-content/uploads/2017/08/Empire_State_Building_New_York_March_2015-188x300.jpg)


![By photophilde (One small step) [CC BY-SA 2.0 (http://creativecommons.org/licenses/by-sa/2.0)], via Wikimedia Commons One_small_step_(3598325560)](http://jdh.hamkins.org/wp-content/uploads/2017/05/One_small_step_3598325560-300x200.jpg)
