I was fascinated recently to discover something I hadn’t realized about relative interpretability in set theory, and I’d like to share it here. Namely,
Different set theories extending ZF are never bi-interpretable!
For example, ZF and ZFC are not bi-interpretable, and neither are ZFC and ZFC+CH, nor ZFC and ZFC+$\neg$CH, despite the fact that all these theories are equiconsistent. The basic fact is that there are no nontrivial instances of bi-interpretation amongst the models of ZF set theory. This is surprising, and could even be seen as shocking, in light of the philosophical remarks one sometimes hears asserted in the philosophy of set theory that what is going on with the various set-theoretic translations from large cardinals to determinacy to inner model theory, to mention a central example, is that we can interpret between these theories and consequently it doesn’t much matter which context is taken as fundamental, since we can translate from one context to another without loss.
The bi-interpretation result shows that these interpretations do not and cannot rise to the level of bi-interpretations of theories — the most robust form of mutual relative interpretability — and consequently, the translations inevitably must involve a loss of information.
To be sure, set theorists classify the various set-theoretic principles and theories into a hierarchy, often organized by consistency strength or by other notions of interpretative power, using forcing or definable inner models. From any model of ZF, for example, we can construct a model of ZFC, and from any model of ZFC, we can construct models of ZFC+CH or ZFC+$\neg$CH and so on. From models with sufficient large cardinals we can construct models with determinacy or inner-model-theoretic fine structure and vice versa. And while we have relative consistency results and equiconsistencies and even mutual interpretations, we will have no nontrivial bi-interpretations.
(I had proved the theorem a few weeks ago in joint work with Alfredo Roque Freire, who is visiting me in New York this year. We subsequently learned, however, that this was a rediscovery of results that have evidently been proved independently by various authors. Albert Visser proves the case of PA in his paper, “Categories of theories and interpretations,” Logic in Tehran, 284–341, Lect. Notes Log., 26, Assoc. Symbol. Logic, La Jolla, CA, 2006, (pdf, see pp. 52-55). Ali Enayat gave a nice model-theoretic argument for showing specifically that ZF and ZFC are not bi-interpretable, using the fact that ZFC models can have no involutions in their automorphism groups, but ZF models can; and he proved the general version of the theorem, for ZF, second-order arithmetic $Z_2$ and second-order set theory KM in his 2016 article, A. Enayat, “Variations on a Visserian theme,” in Liber Amicorum Alberti : a tribute to Albert Visser / Jan van Eijck, Rosalie Iemhoff and Joost J. Joosten (eds.) Pages, 99-110. ISBN, 978-1848902046. College Publications, London. The ZF version was apparently also observed independently by Harvey Friedman, Visser and Fedor Pakhomov.)
Meanwhile, let me explain our argument. Recall from model theory that one theory $S$ is interpreted in another theory $T$, if in any model of the latter theory $M\models T$, we can define (and uniformly so in any such model) a certain domain $N\subset M^k$ and relations and functions on that domain so as to make $N$ a model of $S$. For example, the theory of algebraically closed fields of characteristic zero is interpreted in the theory of real-closed fields, since in any real-closed field $R$, we can consider pairs $(a,b)$, thinking of them as $a+bi$, and define addition and multiplication on those pairs in such a way so as to construct an algebraically closed field of characteristic zero.
Two theories are thus mutually interpretable, if each of them is interpretable in the other. Such theories are necessarily equiconsistent, since from any model of one of them we can produce a model of the other.
Note that mutual interpretability, however, does not insist that the two translations are inverse to each other, even up to isomorphism. One can start with a model of the first theory $M\models T$ and define the interpreted model $N\models S$ of the second theory, which has a subsequent model of the first theory again $\bar M\models T$ inside it. But the definition does not insist on any particular connection between $M$ and $\bar M$, and these models need not be isomorphic nor even elementarily equivalent in general.
By addressing this, one arrives at a stronger and more robust form of mutual interpretability. Namely, two theories $S$ and $T$ are bi-interpretable, if they are mutually interpretable in such a way that the models can see that the interpretations are inverse. That is, for any model $M$ of the theory $T$, if one defines the interpreted model $N\models S$ inside it, and then defines the interpreted model $\bar M$ of $T$ inside $N$, then $M$ is isomorphic to $\bar M$ by a definable isomorphism in $M$, and uniformly so (and the same with the theories in the other direction). Thus, every model of one of the theories can see exactly how it itself arises definably in the interpreted model of the other theory.
For example, the theory of linear orders $\leq$ is bi-interpretable with the theory of strict linear order $<$, since from any linear order $\leq$ we can define the corresponding strict linear order $<$ on the same domain, and from any strict linear order $<$ we can define the corresponding linear order $\leq$, and doing it twice brings us back again to the same order.
For a richer example, the theory PA is bi-interpretable with the finite set theory $\text{ZF}^{\neg\infty}$, where one drops the infinity axiom from ZF and replaces it with the negation of infinity, and where one has the $\in$-induction scheme in place of the foundation axiom. The interpretation is via the Ackerman encoding of hereditary finite sets in arithmetic, so that $n\mathrel{E} m$ just in case the $n^{th}$ binary digit of $m$ is $1$. If one starts with the standard model $\mathbb{N}$, then the resulting structure $\langle\mathbb{N},E\rangle$ is isomorphic to the set $\langle\text{HF},\in\rangle$ of hereditarily finite sets. More generally, by carrying out the Ackermann encoding in any model of PA, one thereby defines a model of $\text{ZF}^{\neg\infty}$, whose natural numbers are isomorphic to the original model of PA, and these translations make a bi-interpretation.
We are now ready to prove that this bi-interpretation situation does not occur with different set theories extending ZF.
Theorem. Distinct set theories extending ZF are never bi-interpretable. Indeed, there is not a single model-theoretic instance of bi-interpretation occurring with models of different set theories extending ZF.
Proof. I mean “distinct” here in the sense that the two theories are not logically equivalent; they do not have all the same theorems. Suppose that we have a bi-interpretation instance of the theories $S$ and $T$ extending ZF. That is, suppose we have a model $\langle M,\in\rangle\models T$ of the one theory, and inside $M$, we can define an interpreted model of the other theory $\langle N,\in^N\rangle\models S$, so the domain of $N$ is a definable class in $M$ and the membership relation $\in^N$ is a definable relation on that class in $M$; and furthermore, inside $\langle N,\in^N\rangle$, we have a definable structure $\langle\bar M,\in^{\bar M}\rangle$ which is a model of $T$ again and isomorphic to $\langle M,\in^M\rangle$ by an isomorphism that is definable in $\langle M,\in^M\rangle$. So $M$ can define the map $a\mapsto \bar a$ that forms an isomorphism of $\langle M,\in^M\rangle$ with $\langle \bar M,\in^{\bar M}\rangle$. Our argument will work whether we allow parameters in any of these definitions or not.
I claim that $N$ must think the ordinals of $\bar M$ are well-founded, for otherwise it would have some bounded cut $A$ in the ordinals of $\bar M$ with no least upper bound, and this set $A$ when pulled back pointwise by the isomorphism of $M$ with $\bar M$ would mean that $M$ has a cut in its own ordinals with no least upper bound; but this cannot happen in ZF.
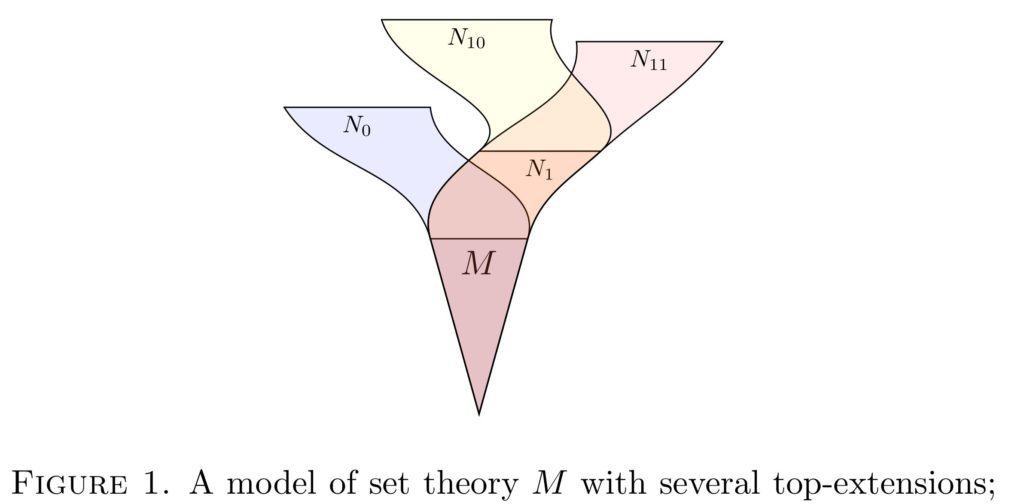
If the ordinals of $N$ and $\bar M$ are isomorphic in $N$, then all three models have isomorphic ordinals in $M$, and in this case, $\langle M,\in^M\rangle$ thinks that $\langle N,\in^N\rangle$ is a well-founded extensional relation of rank $\text{Ord}$. Such a relation must be set-like (since there can be no least instance where the predecessors form a proper class), and so $M$ can perform the Mostowski collapse of $\in^N$, thereby realizing $N$ as a transitive class $N\subseteq M$ with $\in^N=\in^M\upharpoonright N$. Similarly, by collapsing we may assume $\bar M\subseteq N$ and $\in^{\bar M}=\in^M\upharpoonright\bar M$. So the situation consists of inner models $\bar M\subseteq N\subseteq M$ and $\langle \bar M,\in^M\rangle$ is isomorphic to $\langle M,\in^M\rangle$ in $M$. This is impossible unless all three models are identical, since a simple $\in^M$-induction shows that $\pi(y)=y$ for all $y$, because if this is true for the elements of $y$, then $\pi(y)=\{\pi(x)\mid x\in y\}=\{x\mid x\in y\}=y$. So $\bar M=N=M$ and so $N$ and $M$ satisfy the same theory, contrary to assumption.
If the ordinals of $\bar M$ are isomorphic to a proper initial segment of the ordinals of $N$, then a similar Mostowski collapse argument would show that $\langle\bar M,\in^{\bar M}\rangle$ is isomorphic in $N$ to a transitive set in $N$. Since this structure in $N$ would have a truth predicate in $N$, we would be able to pull this back via the isomorphism to define (from parameters) a truth predicate for $M$ in $M$, contrary to Tarski’s theorem on the non-definability of truth.
The remaining case occurs when the ordinals of $N$ are isomorphic in $N$ to an initial segment of the ordinals of $\bar M$. But this would mean that from the perspective of $M$, the model $\langle N,\in^N\rangle$ has some ordinal rank height, which would mean by the Mostowski collapse argument that $M$ thinks $\langle N,\in^N\rangle$ is isomorphic to a transitive set. But this contradicts the fact that $M$ has an injection of $M$ into $N$. $\Box$
It follows that although ZF and ZFC are equiconsistent, they are not bi-interpretable. Similarly, ZFC and ZFC+CH and ZFC+$\neg$CH are equiconsistent, but no pair of them is bi-interpretable. And again with all the various equiconsistency results concerning large cardinals.
A similar argument works with PA to show that different extensions of PA are never bi-interpretable.
On the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I argue that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment.