This will be a lecture series at Peking University in Beijing in June 2025.
Announcement at Peking University
Course abstract. This will be a series of advanced lectures on set theory, treating diverse topics and particularly those illustrating how set theoretic ideas and conceptions shed light on core foundational matters in mathematics. We will study the pervasive independence phenomenon over the Zermelo-Fraenkel axioms of set theory, perhaps the central discovery of 20th century set theory, as revealed by the method of forcing, which we shall study in technical detail with numerous examples and applications, including iterated forcing. We shall look into all matters of the continuum hypothesis and the axiom of choice. We shall introduce the basic large cardinal axioms, those strong axioms of infinity, and investigate the interaction of forcing and large cardinals. We shall explore issues of definability and truth, revealing a surprisingly malleable nature by the method of forcing. Looking upward from a model of set theory to all its forcing extensions, we shall explore the generic multiverse of set theory, by which one views all the models of set theory as so many possible mathematical worlds, while seeking to establish exactly the modal validities of this conception. Looking downward in contrast transforms this subject to set-theoretic geology, by which one understands how a given set-theoretic universe might have arisen from its deeper grounds by forcing. We shall prove the ground-model definability theorem and the other fundamental results of set-theoretic geology. The lectures will assume for those participating a certain degree of familiarity with set-theoretic notions, including the basics of ZFC and forcing.
There will be ten lectures, each a generous 3 hours.
Lecture 1. Set Theory
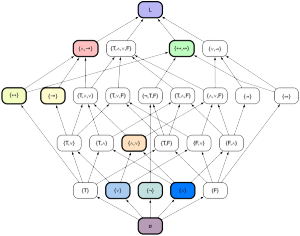
This first lecture begins with fundamental notions, including the dramatic historical developments of set theory with Cantor, Frege, Russell, and Zermelo, and then the rise of the cumulative hierarchy and the iterative conception. The move to a first-order foundational theory. The Skolem paradox. The omission of urelements and the move to a pure set theory. We will establish the reflection phenomenon and the phenomenon of correctness cardinals, before providing some simple relative consistency results. We will compare the first-order approach to the various class theories and also lay out the spectrum of weak theories, including locally verifiable set theory, before discussing countabilism as an approach to set theory.
Lecture 2. Categoricity and the small large cardinals
We will discuss the central role and importance of categoricity in mathematics, highlighting this with results of Dedekind and Huntington, and with several examples of internal categorcity. Afterwards, we shall begin to introduce various small large cardinal notions—the inaccessible cardinals, the hyperinaccessibility hierarchy, Mahlo cardinals, worldly cardinals, other-worldly cardinals. We shall explain the connection with categoricity via Zermelo’s categoricity result. Going deeper, we discuss the possibility of categorical large cardinals and the enticing possibility of a fully categorical set theory.
Lecture 3. Forcing
We shall give an introduction to forcing, pursuing and comparing two approaches, via partial orders versus Boolean algebras. Forcing arises naturally from the iterative conception of the cumulative hierarchy, when undertaken in multi-valued logic. We shall see the principal introductory forcing examples, including the forcing to add a Cohen real, cardinal collapse forcing, forcing the failure of CH, forcing to add dominating reals, almost disjoint coding, iterated forcing, the forcing of Martin’s axiom, and the case of Suslin trees.
Lecture 4. Continuum Hypothesis
We tell the story of the continuum hypothesis, from Cantor’s initial conception and strategy, to Gödel’s proof of CH in the constructible universe, and ultimately Cohen’s forcing of ¬CH, establishing independence over ZFC. The CH is a forcing switch. We discuss the generalized continuum hypothesis GCH, and prove Easton’s theorem on the continuum function. Finally, we discuss various philosophical approaches to settling the CH problem, including Freiling’s axiom and the equivalence with ¬CH, and the role of the continuum hypothesis in providing a categorical theory of the hyperreals. Two equivalent formulations of CH in ZFC are not equivalent without AC.
Lecture 5. Axiom of Choice
We tell the story of the axiom of choice, beginning with a spectrum of equivalent formulations, including the linearity of cardinality. We discuss the abstract cardinal-assignment problem versus the cardinal-selection problem. We establish the truth of the axiom of choice in the constructible universe, as well as global choice, but ultimately the independence of the axiom of choice over ZF via forcing and the symmetric model construction method. Finally, we discuss the perfect predictor theorem and the box puzzle conundrum.
Lecture 6. Definability
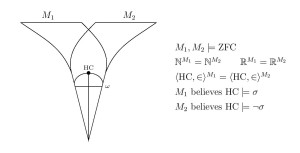
We shall define and discuss the formal notion of definability in mathematics and set theory. Can every set be definable? We exhibit the phenomenon of pointwise definable models and their relevance for the Math Tea argument. We define the inner model HOD and explore its interaction with forcing, forcing V=HOD and also forcing V≠HOD. We reveal the coquettish nature of HOD, establishing the nonabsoluteness of HOD, showing furthermore that every model of set theory is the HOD of another model. We show how forcing generic filters can be definable in their forcing extensions. Finally, we shall exhibit a spectrum of paradoxical examples revealing various subtleties in the notion of definability.
Lecture 7. Truth
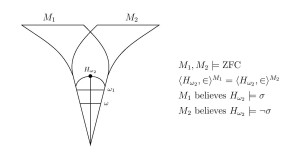
What is truth? We establish Tarski’s theorem on the nondefinability of truth, and establish the second incompleteness theorem via the Grelling-Nelson paradox. We analyze the connection between truth predicates and correctness cardinals. What is the consistency strength of having a truth predicate? Can a model of set theory contain its own theory as an element? Must it? We define the truth telling game. We shall force a definable truth predicate for HOD. We shall establish the nonabsoluteness of satisfaction.
Lecture 8. Forcing and large cardinals
Can large cardinals settle CH? Gödel had hoped so, but this is refuted by the Levy-Solovay theorem. We will prove forcing preservation theorems for large cardinals, and nonabsoluteness theorems. On the difference between lifting and extending measures. Laver indestructibility and the lottery preparation, via master condition arguments.
Lecture 9. Set-theoretic geology
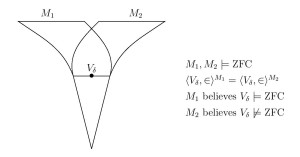
Looking down, we shall give an introduction to set-theoretic geology. We will prove the ground model definability theorem, using the cover and approximation properties. We shall define the Mantle and prove that every model of set theory is the Mantle of another model. We will discuss Bukovski’s theorem characterizing forcing extensions and prove Usuba’s theorems on the downward directedness of grounds.
Lecture 10. Set-theoretic potentialism
Looking up, we view forcing as a modality, viewing every model of set theory in the context of its generic multiverse. We shall investigate the modal logic of forcing with independent buttons and switches. We shall explore the other natural interpretations of set-theoretic potentialism and investigate their modal validities.
Comments or suggestions welcome.




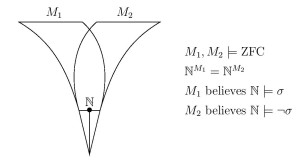 On the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I argue that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment.
On the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I argue that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment. I should like to give a brief account of the argument that KM implies Con(ZFC) and much more. This argument is well-known classically, but unfortunately seems not to be covered in several of the common set-theoretic texts.
I should like to give a brief account of the argument that KM implies Con(ZFC) and much more. This argument is well-known classically, but unfortunately seems not to be covered in several of the common set-theoretic texts.