 This will be a talk for the Computability Theory and Foundations of Mathematics conference at the Tokyo Institute of Technology, September 7-11, 2015. The conference is held in celebration of Professor Kazuyuki Tanaka’s 60th birthday.
This will be a talk for the Computability Theory and Foundations of Mathematics conference at the Tokyo Institute of Technology, September 7-11, 2015. The conference is held in celebration of Professor Kazuyuki Tanaka’s 60th birthday.
Abstract. Recent results on the embeddability phenomenon and universality amongst the models of set theory are an appealing blend of ideas from set theory, model theory and computability theory. Central questions remain open.
A surprisingly vigorous embeddability phenomenon has recently been uncovered amongst the countable models of set theory. It turns out, for instance, that among these models embeddability is linear: for any two countable models of set theory, one of them embeds into the other. Indeed, one countable model of set theory $M$ embeds into another $N$ just in case the ordinals of $M$ order-embed into the ordinals of $N$. This leads to many surprising instances of embeddability: every forcing extension of a countable model of set theory, for example, embeds into its ground model, and every countable model of set theory, including every well-founded model, embeds into its own constructible universe.
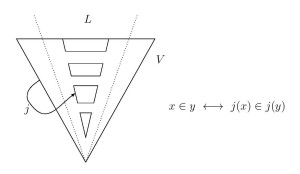 Although the embedding concept here is the usual model-theoretic embedding concept for relational structures, namely, a map $j:M\to N$ for which $x\in^M y$ if and only if $j(x)\in^N j(y)$, it is a weaker embedding concept than is usually considered in set theory, where embeddings are often elementary and typically at least $\Delta_0$-elementary. Indeed, the embeddability result is surprising precisely because we can easily prove that in many of these instances, there can be no $\Delta_0$-elementary embedding.
Although the embedding concept here is the usual model-theoretic embedding concept for relational structures, namely, a map $j:M\to N$ for which $x\in^M y$ if and only if $j(x)\in^N j(y)$, it is a weaker embedding concept than is usually considered in set theory, where embeddings are often elementary and typically at least $\Delta_0$-elementary. Indeed, the embeddability result is surprising precisely because we can easily prove that in many of these instances, there can be no $\Delta_0$-elementary embedding.
The proof of the embedding theorem makes use of universality ideas in digraph combinatorics, including an acyclic version of the countable random digraph, the countable random $\mathbb{Q}$-graded digraph, and higher analogues arising as uncountable Fraïssé limits, leading to the hypnagogic digraph, a universal homogeneous graded acyclic class digraph, closely connected with the surreal numbers. Thus, the methods are a blend of ideas from set theory, model theory and computability theory.
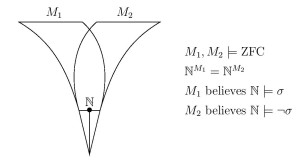
Results from Incomparable $\omega_1$-like models of set theory show that the embedding phenomenon does not generally extend to uncountable models. Current joint work of myself, Aspero, Hayut, Magidor and Woodin is concerned with questions on the extent to which the embeddings arising in the embedding theorem can exist as classes inside the models in question. Since the embeddings of the theorem are constructed externally to the model, by means of a back-and-forth-style construction, there is little reason to expect, for example, that the resulting embedding $j:M\to L^M$ should be a class in $M$. Yet, it has not yet known how to refute in ZFC the existence of a class embedding $j:V\to L$ when $V\neq L$. However, many partial results are known. For example, if the GCH fails at an uncountable cardinal, if $0^\sharp$ exists, or if the universe is a nontrivial forcing extension of some ground model, then there is no embedding $j:V\to L$. Meanwhile, it is consistent that there are non-constructible reals, yet $\langle P(\omega),\in\rangle$ embeds into $\langle P(\omega)^L,\in\rangle$.
CFTM 2015 extended abstract | Article | CFTM | Slides
 Abstract. In light of the comparative success of membership-based set theory in the foundations of mathematics, since the time of Cantor, Zermelo and Hilbert, it is natural to wonder whether one might find a similar success for set-theoretic mereology, based upon the set-theoretic inclusion relation $\subseteq$ rather than the element-of relation $\in$. How well does set-theoretic mereological serve as a foundation of mathematics? Can we faithfully interpret the rest of mathematics in terms of the subset relation to the same extent that set theorists have argued (with whatever degree of success) that we may find faithful representations in terms of the membership relation? Basically, can we get by with merely $\subseteq$ in place of $\in$? Ultimately, I shall identify grounds supporting generally negative answers to these questions, concluding that set-theoretic mereology by itself cannot serve adequately as a foundational theory.
Abstract. In light of the comparative success of membership-based set theory in the foundations of mathematics, since the time of Cantor, Zermelo and Hilbert, it is natural to wonder whether one might find a similar success for set-theoretic mereology, based upon the set-theoretic inclusion relation $\subseteq$ rather than the element-of relation $\in$. How well does set-theoretic mereological serve as a foundation of mathematics? Can we faithfully interpret the rest of mathematics in terms of the subset relation to the same extent that set theorists have argued (with whatever degree of success) that we may find faithful representations in terms of the membership relation? Basically, can we get by with merely $\subseteq$ in place of $\in$? Ultimately, I shall identify grounds supporting generally negative answers to these questions, concluding that set-theoretic mereology by itself cannot serve adequately as a foundational theory.



 On the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I argue that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment.
On the basis of these observations, Ruizhi Yang (Fudan University, Shanghai) and I argue that the definiteness of the theory of truth for a structure, even in the case of arithmetic, cannot be seen as arising solely from the definiteness of the structure itself in which that truth resides, but rather is a higher-order ontological commitment.
 This will be a seminar talk I shall give on March 3, 2016 at the University of Torino, Italy, in the same department where Giuseppe Peano had his position. I shall be in Italy for the dissertation defense of Giorgio Audrito, on whose dissertation committee I am serving as president.
This will be a seminar talk I shall give on March 3, 2016 at the University of Torino, Italy, in the same department where Giuseppe Peano had his position. I shall be in Italy for the dissertation defense of Giorgio Audrito, on whose dissertation committee I am serving as president. This is joint work with Victoria Gitman. See our article,
This is joint work with Victoria Gitman. See our article, ![By PeterPan23 [Public domain], via Wikimedia Commons](https://upload.wikimedia.org/wikipedia/commons/f/fb/Darts_in_a_dartboard.jpg)
.jpg)




 This will be an invited talk for the
This will be an invited talk for the