 This seminar will be a graduate-level survey of topics in logic for philosophers, including propositional logic, modal logic, predicate logic, model theory, completeness, incompleteness, computability theory, set theory and the higher infinite. The material will thus be a mixture of philosophical logic and mathematical logic, and a goal of the course will be to develop the student’s ability to consider these ideas with clarity and precision.
This seminar will be a graduate-level survey of topics in logic for philosophers, including propositional logic, modal logic, predicate logic, model theory, completeness, incompleteness, computability theory, set theory and the higher infinite. The material will thus be a mixture of philosophical logic and mathematical logic, and a goal of the course will be to develop the student’s ability to consider these ideas with clarity and precision.
The lectures will be largely self-contained, and some course materials will be distributed during the semester. On some topics, material will be drawn from:
More Precisely, The Math You Need to do Philosophy, Eric Steinhart, Broadview.
On other topics, students may wish to supplement the lecture notes with other sources, and there are dozens of suitable texts for this purpose, as well as on-line information.
For focused help, students are also directed to the following excellent on-line resources:
- Math.StackExchange.com, an on-line question/answer forum for mathematics questions, which welcomes questions on logic, and most questions get high quality answers very quickly.
- MathOverflow.net, a similar site for research-level mathematics questions.
Weekly exercises. Exercises will be assigned in connection with each lecture, and these are due by the following lecture. It is fine and even advisable for you to work in groups, but kindly submit only solutions that you yourself have thoroughly mastered.
Final paper. Students will write a final paper (about 8 pages) on an approved topic chosen in consultation with the instructor. The instructor’s goal in assigning this paper is to give the students experience both in conducting research on a technical topic, as well as in writing on such a topic. Suitable topics will be suggested, but they will generally consist not of giving a summary account or criticism of an advanced topic from the literature (this will be discouraged), but rather of considering a modest but novel topic or context—perhaps a variation of a better known theory—and then discovering and working out some interesting aspect of it. The idea is that the paper topic should be a little like undertaking research in logic. The paper is due by the last day of the semester, and late work will not be accepted.
Grading. Grades will be based on the weekly exercises and the final paper (with a class participation element). All work for this class, including the final paper, must be submitted by the last day of the semester. No Incomplete grades will be given—no exceptions.
My intention is to post the weekly problem sets here, by updating this post. I will make Google+ posts pointing to this page when it is updated, for a circle of subscribed members; send me a message on G+ to join the circle (or you can alternatively just subscribe to this blog, but then you’ll get notified of all my posts).
Lecture 1. A picture of logic. Propositional logic. Truth tables; tautologies; logical equivalence; well-formed formulas; induction on formulas; complete sets of connectives; every truth function is represented by a formula in disjunctive normal form; satisfiability; connections with P vs. NP.
Lecture 1 notes by a student
Exercises:
1. Make truth tables for
2. Argue that every well-formed formula of propositional logic has the same number of left as right parentheses. (According to the rules we gave in class for the formula-building operations.)
3. Argue that every well-formed formula of propositional logic has twice as many parentheses as binary logical connectives.
4. Argue that the collection of tautologies is closed under conjunction, disjunction, implication and biconditional. In other words, if and are tautologies, then so are , , and .
5. Which of the converses of these are true? In other words, which of the following are correct:
- If is a tautology, then and are tautologies.
- If is a tautology, then and are tautologies.
- If is a tautology, then and are tautologies.
- If is a tautology, then and are tautologies.
6. Argue that every propositional assertion is logically equivalent to an assertion in conjunctive normal form (a conjunction of disjunction clauses, each of which is a disjunction of literals). (Hint: in class we proved that every propositional assertion is logically equivalent to an assertion in disjunction normal form. Given , consider in light of what we did in class.)
7. Determine which of the following sets of logical connectives are complete: , . (The second one is a bit harder, and we’ll cover it in class next time.)
8. Show that Nand and Nor are the only binary connectives that, by themselves individually, are complete. (Hint: if you have a binary connective that is complete, then consider what the truth table of must be. What must it be on the top row? On the bottom row? How many possibilities remain?)
Possible paper topic connected with the Satisfiability problem and P vs. NP. For example, you could write a paper explaining how the general satisfiability problem reduces to the 3-Sat problem. (This is a classical result, but one that can be easily rediscovered independently.)
Lecture 2. Discussion of homework problems from last time, including a simple account of the disjunctive normal form theorem and the conjunctive normal form theorem.
New topic: multi-valued logic; Lukasiewicz/Kleene logic. Basic truth tables for 3-valued logic. Discussion of various motivations, such as logic of missing information, logic of possible worlds, logic of unknown truth values, neither true nor false, both true and false; most of these stories are flawed and do not actually capture the logic. Tautologies and complete sets of connectives in 3-valued logic. Notions of logical equivalence. No strict tautologies. Disjunctive normal form still works. Weak tautologies are the same as classical tautologies.
Lecture 2 notes by a student
Exercises.
- If is a propositional assertion in the language with , and . Does there always exist a crispification of to with and another crispification with ? In other words, does the truth value mean that it could have been and it could have been , depending on what way the input values are made crisp?
- Define a natural analogue of NAND and of NOR for Kleene logic. Does it obey the expected identities? Does it continue to be complete in Kleene logic in the narrow sense? In the wide sense?
- Verify the De Morgan laws in Lukasiewicz logic, namely, that and , using to mean logically equivalent in the sense of having the same truth table.
- Verify the distributivity laws in Lukasiewicz logic. (You probably don’t want to compute the truth table, since it has 27 rows; rather, reason about what must happen if is true; if is false; and if is .)
- Find an expression in , and that has value , if any of them is , and otherwise has value .
- Is the truth table of every expression in Lukasiewicz logic determined (as it is in classical logic) by the location of the ’s? That is, if you know where the ’s are, can you determined whether the others are or , just from knowing that the expression came from ?
Possible paper topics.
- Develop the logic of missing information. The context would be that there is a genuine classical logic world, but we do not know some of the truth values of the atomic facts. What is a sensible way to develop a logic for this situation? Is it truth-functional? Can we assign truth values to every statement in a sensible multi-valued logic? What are the notions of tautology, validity, completeness, and so on?
- Explore the notion of complete sets of logical connectives in Lukasiewicz logic. We know the standard set of connectives is not complete, but can we augment it with another connective to make it complete? Is there a single connective in the 3-valued logic that is complete? (I have some good references for research on this topic.)
Lecture 3. Fuzzy logic. Definitions of the logic. Disjunctive normal form theorem. Traditional connectives are not complete. No finite set (nor even any countably infinite set, nor even any set of size continuum) is complete for fuzzy logic. Tautologies in fuzzy logic; weak tautologies (truth value ); positive assertions (truth value is never ). For assertions in traditional logical language, weak tautologies, positive and classical tautologies are the same. The proof uses logical homomorphisms, translating fuzzy logic to Lukasiewicz logic. We discussed various kinds of logical homomorphisms. General treatment of truth-functional logic: a space of truth values, with logical functions on that space. Concepts of extensions and logical homomorphisms . Boolean algebras. Axioms of Boolean algebras. A few examples, including power sets.
Exercises.
- Verify in fuzzy logic that
- Verify that the de Morgan laws continue to hold in fuzzy logic.
- Verify that the distributivity laws continue to hold in fuzzy logic.
- Argue that in fuzzy logic, just as in Lukasiewicz logic, there are no tautologies in the language having only the traditional five connectives: .
- Consider the translation from fuzzy logic to Lukasiewicz logic, which takes the center interval of fuzzy truth values to the truth value U; the numbers in the interval to and numbers in to . Show that this is a logical homomorphism of fuzzy logic to Lukasiewicz logic.
- Show that there is no logical homomorphism of fuzzy logic to classical logic.
- Discuss the question of whether fuzzy logic is the logic of probabilistic reasoning. Suppose that we are in a probability space, where the underlying propositional variables are given a probability. Does fuzzy logic then give sensible probabilities for compound logical expressions using those variables? That is, if we know the probabilities of , and , then does fuzzy logic tell us the probability of compound expressions like ?
Suggested Paper topics.
- Investigate the nature of the fuzzy truth functions that one may define using the standard five connectives. Can one recognize or characterize them? How many binary connectives are realized?
- Investigate and discuss the issue of continuity of truth functions in fuzzy logic. Under what kind of semantics would one want to make use of or consider discontinuous truth functions?
- Discuss the issue or ordinal comparision versus cardinal comparison in fuzzy logic truth values. One might consider logical homomorphisms of fuzzy logic to itself, which preserve the order of truth values, but which greatly magnify small differences or diminish large ones.
Lecture 4. Relational logic; the theory of relations. Reflexivity, symmetry, transitivity; irreflexivity; asymmetry; anti-symmetry; anti-transitivity; equivalence relations; equivalence classes; partitions; every equivalence relation determines a partition and vice versa. Refinement of equivalence relations. Partial orders; strict orders; converse order; pre-order; comparability.
Lecture 4 student notes
Exercises.
- Are all eight combinations of the properties of reflexivity, symmetry and transitivity possible? Provide instances of relations exhibiting each combination that can occur.
- Criticize the following argument that every relation that is symmetric and transitive is also reflexive: If is symmetric, then implies , and so if it is also transitive, it follows that , and so it is reflexive. Is this argument correct? If not, what is a correct statement that a similar argument establishes?
- How are the concepts of asymmetric, anti-symmetric and “not symmetric” connected to each other? Which imply which others? Which of the eight conceivable combinations actually arise? Provide relations exhibiting each possible combination.
- How many equivalence relations are there on a 4 element set? It is possible easily to draw a small picture of each one. Organize this chart into the refinement hierarchy.
- Consider the claim that the living-in-the-same-city-as relation refines the living-in-the-same-country-as relation, on the set of all people. Discuss the various problematic assumptions underlying this example. For example, if there were a person who lives in more than one country, or no country, or a person who lives in more than one city, or no city; or suppose that there is a city with parts in more than one country. For each of these situations and others you may think of, precisely which parts of the claims that these relations are both equivalence relations on the set of all people and that the first relation refines the second would be affected?
- Consider the relation of comparability for elements in a partial order. Is it an equivalence relation? Consider each of the properties of relations that we have considered (reflexive, irreflexive, symmetric, asymmetric, anti-symmetric, etc.) and argue that comparability always has that property or give an example partial order showing that the comparability relation need not have that property.
Lecture 5. Order theory. Mathematical and natural examples. Reflexive closure of a relation. Symmetric closure. Transitive closure. The reflexive/transitive closure of a relation is the same as the reachability relation. Strict partial orders. Defining from and vice versa. Pre-orders (quasi-orders). With pre-orders, the interdefinability of with breaks down. Example of distinct preference pre-orders with same strict preferences. Maximal and greatest elements. Minimal and least elements. Example of a partial order with a unique maximal element that is not greatest. Upper bounds; lower bounds; least upper bounds; greatest lower bounds. Lattices. Linear orders. Linearly graded partial orders.
Lecture 5 student notes
Exercises.
- Give an example of an anti-symmetric relation, whose reflexive/transitive closure is not anti-symmetric.
- Give a relation on five elements, using as few relational instances as possible, whose reflexive/transitive closure is the full relation (for which each of the five elements stands in the relation to all five elements). How many relational edges did you use? Can you make a general claim and argument for a domain with elements?
- Suppose that is a partial pre-order. Define just in case and . Argue that is an equivalence relation on the same domain.
- Does the interdefinability of and succeed with pre-orders? Suppose that is a transitive reflexive relation (that is, a pre-order). Define if and . Will this necessarily be a partial order? If not, what is a better way to define a strict partial order in terms of for a pre-order ?
- Suppose that an author (mistakenly, in my view) defines that we are {\it indifferent} between and if neither nor is better than the other. That is, . Provide a preference relation for which this is not an equivalence relation. Specifically, we’d want the person to be indifferent between and , and indifferent between and , but not indifferent between and .
- True or false: if is a partial ordering on a set, then if and only if .
- Give an example of a partial order that admits more than one linear grading order. In other words, provide a partial order that can be divided into levels in more than one way.
Suggested paper topics.
- The connection between preference relations and group preferences. For example, if you try to define a group preference by using majority rule on the individual preferences, then you don’t necessarily get a partial order.
- The algebra of partial orders. If and are partial orderings, there is a notion of , which is the order placing a copy of on top of a copy of ; and is the order consisting of many copies of . There are numerous easy but interesting questions to ask about how features are preserved or not by these constructions, such as: if and are dense orders, then are also dense? ? And what of discrete orders?
Lecture 6. First-order predicate logic. Formal language of a relational structure. Well-formed formulas. Induction on formulas. Parse trees. Unique readability. Free and bound variables. Scope. Sentences. Definition of satisfaction. Truth in a model.
Lecture 6 student notes
Exercises.
- In the language of the structure , construct a formula with two free occurrences each of the variable symbols , and , and with two bound occurrences of and , but where the bound appearances of fall under the scope of different quantifications over . Next, construct a second formula with variables each with one free occurrence and three bound occurrences, but make the bound occurrences of , respectively, fall under the scope of different quantifiers of these variables.
- Distinguish the structure , where denotes the positive integers and just in case divides , from the structure , where is the collection of finite subsets of the natural numbers . That is, find a statement in the first-order language with one binary relation, which is true in and false in .
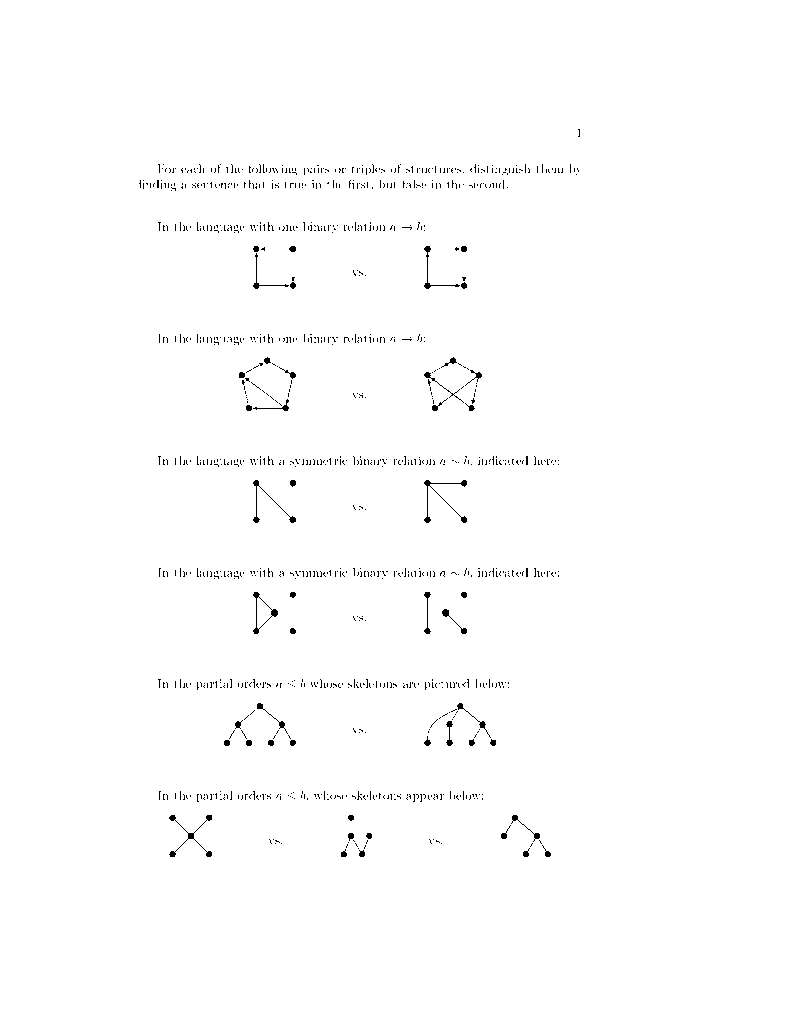
- For each of the following pairs or triples of structures, distinguish them by finding a sentence that is true in the first, but false in the second.
Lecture 7. Signatures in first-order logic, with constants, functions and relations. terms. Models. Satisfaction. Distinguishing various structures by sentences. (Aside on the irrationality of .) The type of an element. Submodels. Reducts. Expansions. Elementary submodels. Leibniz principle on identity of indiscernibles. Leibnizian models. Isomorphisms. Elementary embeddings.
Lecture 7 students notes
Exercises.
- Kindly do the rest of problem 3 from lecture 6 above; some of those instances were not mentioned in the previous lecture.
- Distinguish the following structures in the first-order language having only multiplication, by finding for each structure a sentence true only in that structure:
- Show that is irrational. (Hint: follow the argument for given in lecture, but replace talk of even/odd with talk involving divisibility-by-. After all, a number is even just in case it is divisible by .) What do you think is the general fact concerning whether is irrational for natural numbers ?
- Consider the chain of submodels Are any of these submodels elementary submodels?
- Argue that is Leibnizian (any two elements are discernible, that is, they have different types).
- Let be a relational structure in which is an equivalence relation. Show that if , then and are indiscernible in this structure.
- Give an example of an infinite pre-order, which is not a partial order, in which any two elements are indiscernible.
- Using some of the examples from the other exercises, find a structure and a submodel such that but .
- In the integers, is less-than fundamentally different from greater-than? Compare with . Are there any statements that can tell apart from ? Specifically, argue that the structures and satisfy exactly the same truths. Conclusion: no first-order assertion can tell apart from . That is, .
Paper topics.
- Indiscernibility and identity. Objects in a model are indiscernible with respect to a given formal language, if they satisfy all the same formulas in that language. There are numerous examples of structures having indiscernible non-identical elements, or in which all elements are indiscernible or none are, and it would be an interesting project to find examples illustrating the range of possibility.
- Is every structure characterized by the collection of first-order truths in it? Is this true for finite structures? This is actually a deep topic, and there are many interesting examples and ideas.
Lecture 8. Definability. Definable elements, definable subsets. Examples with small finite partial orders. Every element of is definable. No element of is definable. Homomorphisms, isomorphisms, automorphisms. If every object is definable, then the structure is Leibnizian. Is the converse true? No. Example of a Leibnizian structure with non-definable elements. is definable in , but not in . The Peano structure . This structure admits elimination of quantifiers, by an argument proceeding via induction on formulas.
Exercises.
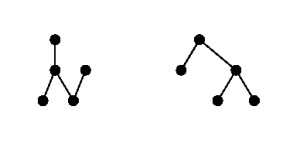
- Which are the definable elements of the following partial orders? For each definable element, provide a definition; if an element is not definable, explain how you know that.
- Consider the case of an equivalence relation having exactly one class of size one, exactly one class of size two, exactly one class of size three, etc. Are there any definable elements? What are the definable subsets?
- Show that every element is definable in . (Hint: it is easy to define ; to define , note that cannot be written as the sum of two other numbers, neither of which are ; now use to define all other numbers.)
- Show that multiplication is not definable from addition in . (Hint: If it were, then would be definable. But argue that is not definable in .)
- Show that “ is even” and “ is odd” are definable in . Using the elimination of quantifiers result from lecture, conclude that is not definable in the Peano structure .
- Show that “ is prime” is definable in .
Suggested Paper topics.
- Additional instances of elimination of quantifiers. For example, in , which is an interesting argument.
- Argue that in a finite structure, Leibnitzian is the same as every-object-is-definable.
- Discuss the Leibnitizian axiom of set theory: every two objects are discernible over the ordinals.
- On the significance of Tarski’s theorem that admits elimination of quantifiers. Discuss significance of having a decision procedure for Cartesian plane geometry.
Lecture 9. Continuation of quantifier elimination. Discussion of Tarski’s theorem on quantifier elimination for , and consequent decidability of Cartesian geometry. Modal logic. Examples of natural modalities. Kripke semantics. Kripke models for propositional modal logic. Kripke frames. Axiom K and axiom Dual are true in all Kripke models. Axiom S is valid on a frame just in case the frame is reflexive. Seriality D is valid on a frame just in case the frame has no terminal worlds, accessing no other worlds. Axiom 4 is valid on a frame just in case the frame transitive. Axiom 5 is valid on a frame just in case the frame is symmetric. Axiom (.2) expresses that the frame is directed. Axiom (.3) expresses that the frame is linear. Predicate modal logic. The Barcan formula and the converse Barcan , and the connection with growing vs. shrinking worlds.
Exercises.
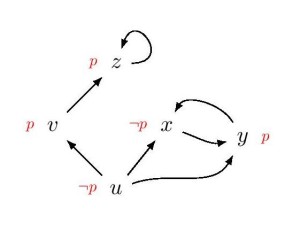
- Determine the truth of the following assertions at the various worlds in the following Kripke model.
- Prove that every assertion of propositional modal
logic is equivalent under the Kripke semantics to an assertion using only
.
- Show that is valid on a partial pre-order frame just in case the frame is directed.
Paper topics. We have fewer exercises because it is time to be working on your papers. Please make an appointment to discuss your topic with me, if you have not done so already.
- Combine modal logic Kripke semantics with multivalued logic.
- Investigate predicate modal logic, such as conditions for the Barcan formula and for its converse.
- Bimodalities obtained by using the accessibility relation and its inverse.
- Analyze various conceptions of temporal logic using modal logic, and investigate how one’s conception of the nature of possibility through time (such as linear, tree branching, others) arise in the resulting modal logic.
Lecture 10. Theory theory. . Deduction theorem for logical consequence: . The set of models of a theory, . The theory of a model . The theory of a set of models, . . . . . . Consequences of a theory. Complete theory. Satisfiable theory. Finitely satisfiable theory. Compactness theorem: A theory is finitely satisfiable if and only if it is satisfiable. Direct proof of compactness using Henkin constants. Every finitely satisfiable theory is contained in a finitely satisfiable complete Henkin theory. Every such theory has a model, built from the Henkin constants. Consequences of compactness. Finiteness is not first-order expressible. Every theory with arbitrarily large finite models has an infinite model. Upward Löwenheim-Skolem theorem. Elementary extensions of . Nonstandard analysis. Infinitesimals. Historical significance of nonstandard analysis for calculus.Lecture 10 student notes
Exercises.
- Show that , if is any set of models.
- Let , the set of consequences of a theory . Show that if and only if .
- Show that a theory is closed under consequences (that is, implies ) if and only if . (Edit: an earlier version of this exercise was not correct.)
- Show that if , then there is a finite subtheory such that . In another words, if a statement is a consequence of a theory , then there is a finite part of the theory that is responsible for this.
Suggested paper topics.
- Nonstandard analysis. There are many topics here that would be suitable; please come and discuss with me. Using the compactness theorem, one could establish that various kinds of nonstandard natural exist.
- Undertake some theory theory in infinitary logic. Prove that compactness can fail; finiteness is expressible and so on.
Lecture 11. Proof theory. What is a proof? Various formal proof systems. Logical axioms, rules of inference, formal proof. Automated theorem proving. Importance of (1) soundness implies ; (2) completeness implies ; (3) decidability: we should be able to recognize whether something is a proof. The MM proof system (A. Miller) is sound and complete. Another more satisfactory proof system, with examples. Gödel’s completeness theorem, using Henkin’s proof. Every consistent theory can be extended to a complete consistent Henkin theory, and every such theory is satisfiable.
Lecture 11 students notes
Exercises.
- Construct a formal proof system that is sound, but not complete.
- Construct a formal proof system that is complete, but not sound.
- Construct a formal proof system that is sound and complete, but not decidable. (These first three exercises are meant to be very easy, and there is no need for the systems to be complicated at all. Think along the lines of having a system with no logical axioms or with every statement being an axiom or with having lots of rules of inference, or none. The right combinations will make the examples work.)
- Show that a theory is inconsistent (proves a contradiction for some ) just in case for every .
- Extra: Show that every formal proof system is equivalent to a formal proof system having no logical axioms. (Hint: add extra rules of inference with empty hypotheses.)
- Extra: Show that any formal proof system having no logical axioms and having rules of inference only with nonempty hypotheses, is not complete. (Hint: consider the proofs arising from the empty theory.)
- Extra: Show that no sound formal proof system having only logical axioms and no rules of inference is complete.
Suggested paper topics.
- Design your own formal proof system and prove the completeness theorem for it.
- Translating proofs from one system to another.
- Automated reasoning. Learn one of the standard proof-checker automated theorem proving systems and carry out a nontrivial formal proof in it.
 Lecture 12. Computability theory. Primitive recursive functions; composition; primitive recursion, with examples. Turing machines. Sample programs. Other computational models: register machines, flowchart machines, recursive functions, idealized programming languages. Hierarchy vision of computability vs. threshold vision. Church-Turing thesis (weak and strong). Undecidability of the halting problem.
Lecture 12. Computability theory. Primitive recursive functions; composition; primitive recursion, with examples. Turing machines. Sample programs. Other computational models: register machines, flowchart machines, recursive functions, idealized programming languages. Hierarchy vision of computability vs. threshold vision. Church-Turing thesis (weak and strong). Undecidability of the halting problem.
Lecture 12 student notes
Exercises
- Write a Turing machine program to compute the function , when is even; otherwise, , when is odd.
- Extra: Explain how the the class of Turing computable functions avoids the diagonalization argument of Gödel given for the primitive recursive functions. That is, we may still effectively enumerate all computable functions, and still attempt to define . Does this argument show that there are intuitively computable functions that are not Turing computable? Why does it work with primitive recursive functions and not with computable functions?
Paper topics
- Develop a new model of computability and prove that it is Turing complete.
- Topics in oracle computation and the Turing degrees.
- Topics in infinitary computability, such as Blum-Shub-Smale machines, or infinite time Turing machines.
Next week: Gödel’s incompleteness theorems!
Lecture 13. Gödel’s incompleteness theorems. Hilbert program. Proof of first incompleteness via halting problem (due to Kleene). For any true computably axiomatizable theory , there is a Turing machine program and input such that does not halt on input , but does not prove this. MRDP theorem. Arithmetization of syntax. Gödel codes. Carnap’s fixed-point lemma. Gödel sentence, “I am not provable.” First incompleteness theorem. Second incompleteness theorem. Derivability conditions. Rosser’s theorem. Tarski’s theorem. Löb’s theorem. Independence phenomenon. Goodstein’s theorem. Kirby-Paris Hydra theorem.
Lecture 13 student notes
Exercises.
- Show that if is a computably axiomatizable theory extending PA, then is inconsistent just in case proves .
All students should be working on their final papers, with the topic chosen in consultation with me. The papers are due by the end of finals week; no late work will be accepted. Please come to my office with drafts for comments and suggestions.
 Lecture 14. Set theory and the higher infinite. The googol plex bang stack hierarchy. Hilbert’s hotel. Countable sets. Cantor’s theorem on the uncountability of the reals. Equinumerosity. Cantor-Schröder-Bernstein theorem. Ordinals. How to count. Cantor’s theorem that . General Comprehension principle. Russell’s paradox. Rise of ZFC. The continuum hypothesis. Gödel’s theorem on the constructible universe; Cohen’s development of forcing. The independence phenomenon. The singularist/pluralist debate in the philosophy of set theory.
Lecture 14. Set theory and the higher infinite. The googol plex bang stack hierarchy. Hilbert’s hotel. Countable sets. Cantor’s theorem on the uncountability of the reals. Equinumerosity. Cantor-Schröder-Bernstein theorem. Ordinals. How to count. Cantor’s theorem that . General Comprehension principle. Russell’s paradox. Rise of ZFC. The continuum hypothesis. Gödel’s theorem on the constructible universe; Cohen’s development of forcing. The independence phenomenon. The singularist/pluralist debate in the philosophy of set theory.
Lecture 14 student notes
This was the last lecture; it was a great time! Final papers are due by the end of finals week. Please drop by my office for comments on a draft version of your paper.
Final Papers The students all wrote final papers on various topics connected with the seminar, and many of them were quite interesting. Let me summarize here several of the resulting titles and topics.
Mala Chatterjee, Łukasiewicz Logic & Strong Completeness. Mala investigates complete sets of connectives for Łukasiewicz logic, introducing several novel connectives, denoted by , and , which she shows can form various small complete sets of connectives for this logic.
Hugo Dumoulin, Logic Gates and the Turing Machine. Hugo constructs a subtractor using only logic gates and explains how logic gates can be used be used to simulate Turing machines.
Arden Koehler, Definability and distinguishability in finite and infinite structures. Arden investigates the difference between Leibnizian structures (where any two objects have different types) and pointwise-definable structures (where every individual is definable) in first-order logic. In finite structures, the concepts are equivalent, but there are infinite structures, even in a finite language, which are Leibnizian, yet have no definable elements.
Annette Martin, A brief look at nonstandard models of true arithmetic. Annette develops the theory of nonstandard models of true arithmetic, establishing the overspill principle, determining the order type of every countable nonstandard model of arithmetic, proving that every nonstandard model of arithmetic has entire chains consisting of composite nonstandard numbers, and proving that there are uncountably many pairwise non-isomorphic countable nonstandard models of true arithmetic.
Nathan Pensler, What is the Logic of Missing Information? Abstract: Is there a logic of missing information? In this paper, I’ll survey several logics and determine
whether any of them provide an adequate analysis of the concept. I first discuss Kleene and Łukasiewicz Logics. I argue that both systems fail as logics of missing information, due to counterexamples involving classical tautologies. I then discuss several new logics of missing information, all of which assign truth values to formulae relative to an informational background. I define what it is for a logic to be truth functional and prove that several logics of this type are truth functional just in case the informational background is severely restricted. I then explore a truth-functional logic of missing information. I conclude by exploring whether there is reason to prefer the truth functional logic of missing information to the non-truth functional logics.
David Storrs-Fox, The modal logic of a knight in chess. David investigates the modal logic of a knight’s move, by considering the frame consisting of the squares on a chessboard (in both the finite and infinite cases) as the possible worlds and the knight’s move as the accessibility relation. After settling a large number of validities and invalidities for this chessboard interpretation, David proves that the squares on the 8×8 chessboard are distinguished by their modal validities, unless they are in rotational or reflective symmetry.
Casey Tirschfield, Select limitations of infinitary logic. In this paper, Casey develops the basic syntax and semantics of the infinitary logics and proved that the compactness theorem and the upward Löwenheim-Skolem theorems can both fail in the infinitary context.
Kameryn J Williams, Complete sets of connectives for generalized Łukasiewicz logics. Abstract: While , , form complete set of connectives for classical propositional logic, this does not hold for Łukasiewicz’s three-valued propositional logic, nor its generalization to -valued logic. We define a unary connective so that , , , form a complete set of connectives for -valued Lukasiewicz logic. We discuss generalizations of this to infinitary logics. If we allow infinite conjunctions and disjunctions of arbitrary size, this provides a complete set of connectives for real-valued Łukasiewicz logic. Restricting to countable conjunctions and disjunctions, the truth functions expressible with these connectives are precisely the Borel functions.
Jake Zuehl, What group preferences can arise by majority vote? It is known by the Condorcet paradox that the group preferences determined by majority vote can be non-transitive, even when all individuals have linearly ordered preference relations. But exactly which relations can arise? In this paper, Jake proves that it is all and only the asymmetric irreflexive relations that arise as the majority-vote group preference relation by a group of individuals with linear preferences. He then proceeds to investigate bounds on the minimum number of voters required to realize a given relation.











![Laurent de La Hyre [Public domain], from Wikimedia Commons](http://jdh.hamkins.org/wp-content/uploads/2018/08/Legion_of_Honor_05.jpg)









